Question

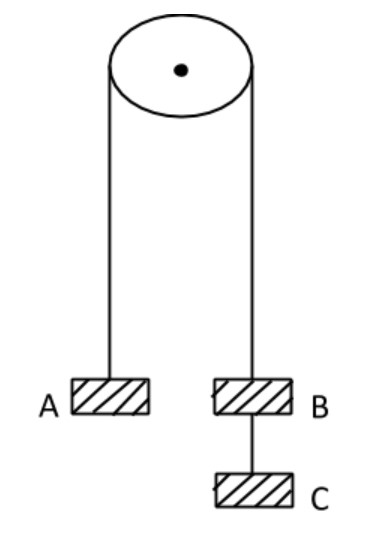
These equal weights of mass 2kg each are hanging on a string passing over a fixed pulley as shown in the figure. What is the tension in the string connecting the weight B and C.
(A) zero
(B) 13.33N
(C) 3.3N
(D) 19.6N

Answer 1

Hint: Tension is a face that always is directed away from the pulley. Hence the masses will be moving. The blocks B and C will move down, and block A will move up.

Complete step by step solution:
Given that \[{m_A} = {m_B} = {m_c} = 2kg\]
All the three blocks will move with the same acceleration in this case of not, they will collide with each other.
Therefore \[{a_A} = {a_B} = {a_c} = a\]
To determine the value of tension, it is essential to first determine the value of acceleration of the blocks.
Since there are many forces that are acting on each block in different directions, let us first assign sign convention, let us consider all the downward acting forces to be as positive, and all the upward acting forces to be as negative.

Since all three blocks have the same mass and acceleration, the net force on all three blocks will be same.

Blocks A and B are directly connected to the same string. Hence \[{T_A} = {T_B} = T\]
Writing the net force equation for each block we get
 \[
  {F_A} = - {m_A}a = {m_A}g - T \\
   \Rightarrow T = {m_A}\left( {g + a} \right) = 2\left( {g + a} \right)..............\left( 1 \right) \\
  {F_B} = {m_B}a = {m_B}g - T + {T_C} \\
   \Rightarrow T = {m_B}\left( {g - a} \right) + {T_C} = 2\left( {g - a} \right) + {T_C}...............\left( 2 \right) \\
  {F_C} = {m_C}a = {m_C}g - {T_C} \\
   \Rightarrow {T_C} = {m_C}\left( {g - a} \right) = 2\left( {g - a} \right)...........\left( 3 \right) \\
 \]
Equating equation (1) and (2) we get
 \[
  2\left( {g + a} \right) = 2\left( {g - a} \right) + {T_C} \\
  2g + 2a = 2g - 2a + {T_C} \\
  {T_C} = 4a \\
 \]
Substituting TC in equation (3) we get
 \[
  4a = 2\left( {g - a} \right) \\
  \Rightarrow 4a = 2g - 2a \\
  \Rightarrow 6a = 2g \\
  \Rightarrow a = \dfrac{9}{3} \\
 \]

Hence, \[{T_C} = 4\left( {\dfrac{9}{3}} \right) = 4\left( {\dfrac{{10}}{3}} \right) = 13.3N\]
Therefore the correct option is (B).

Note: Sign convention can also be taken the other way sound as mentioned in the solution. Perspective of which method of sign convention is used, we get the same answer.