Question

There is an infinite wire grid with cells in the form of equilateral triangles. The resistance of each wire between neighbouring joint connections is $\mathrm{R}_{0}$. The net resistance of the whole grid between the points A and B as shown is:

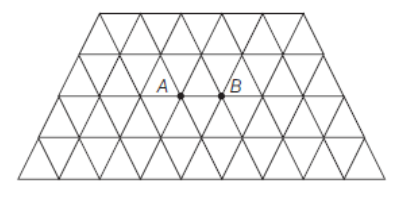
a. $\mathrm{R}_{0}$
b. $\dfrac{R_{0}}{2}$
c. $\dfrac{\mathrm{R}_{0}}{3}$
d. $\dfrac{\mathrm{R}_{0}}{4}$

Answer 1

Hint: To answer this question we need to know the concept of the superposition theorem. The superposition principle states that in case there are two or more than two waves that will overlap in the space, the sum of the resultant disturbance from the overlapping will be similar to that of the algebraic sum of the overlapping waves considered individually.

Complete step by step answer:
First let us consider if ‘I’ amount of current enters at ‘A’. Then we can write that:
$\dfrac{\mathrm{I}}{6}$ will flow through $\mathrm{AB}$.
Now, in the second case, let the current be extracted from B, again current $\dfrac{\mathrm{I}}{6}$ will flow through $\mathrm{AB}$.
Now, if simultaneously current enters at A and leaves at B, then the current $\dfrac{\mathrm{I}}{6}+\dfrac{1}{6}=\dfrac{\mathrm{I}}{3}$ should flow through $\mathrm{AB}$.

Now we can write that the current will be: $\mathrm{I}-\dfrac{\mathrm{I}}{3}=\dfrac{2 \mathrm{I}}{3}$ that will flow through the remaining part.
Now, let us consider the resistance of the remaining part will be: $\mathrm{R}_{1}$
Hence, the expression that can be formed is:
Now $\dfrac{\mathrm{R}_{0} \mathrm{I}}{3}=\dfrac{\mathrm{R}_{1} 2 \mathrm{I}}{3}$
$\mathrm{R}_{0}=2 \mathrm{R}_{1}$

Hence the expression is formed as:
$\mathrm{R}_{\mathrm{eq}}=\dfrac{\mathrm{R}_{1} \mathrm{R}_{0}}{\mathrm{R}_{1}+\mathrm{R}_{0}}$
$=\dfrac{\mathrm{R}_{1} 2 \mathrm{R}_{1}}{\mathrm{R}_{1}+2 \mathrm{R}_{1}}$
After the evaluation we obtain the final expression as:
$=\dfrac{2 \mathrm{R}_{1}}{3}$
$=\dfrac{\mathrm{R}_{0}}{3}$

Hence, the correct answer is option (C).

Note: We should keep in mind that in order to calculate the total amount of current in any part of the linear circuit which will be equal to that of the algebraic sum of all the currents that will be formed in each of the sources that is considered separately. The separate currents are to be combined and then replaced with specific voltage sources by all the short circuits and then every other current source will be replaced by open circuits.