Question

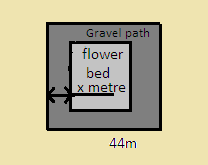
There is a square field whose side is $44$ m. A square flower bed is prepared in its centre leaving a gravel path all around the flower bed. The total cost of laying the flower bed and grazing the path, at Rs.$2.75$ And Rs. $1.50$ per square meter respectively, is Rs. $4904$. Find the width of the gravel path.

Answer 1

Hint: First assume the width of gravel path to be x m and. Then each side of the flower bed will be beside a square field- $2$(width of gravel).Find area of the flower bed and gravel path, then multiply these areas by their respective rate and add them. Equate the added terms to the cost of laying the flowerbed and gravel path. Solve for x.

Complete step-by-step answer:
 Let us assume the gravel path’s width to be x m. Since the flower bed is in the centre of the square field with a gravel path surrounding it. So each side of the flower bed is= side of a square field- $2$(width of gravel).
$ \Rightarrow $ Each Side of the flower bed=$44 - 2{\text{x}}$ m
Then the area of flower bed=${\left( {44 - 2{\text{x}}} \right)^2}$ m {as the area of square=${\text{sid}}{{\text{e}}^2}$}
And the area of the square field =$44 \times 44 = 1936$ sq.m.
Then the area of gravel path=area of square field-area of flower bed
$ \Rightarrow $ Area of gravel path=$1936 - {\left( {44 - 2{\text{x}}} \right)^2} = 1936 - 1936 + 176{\text{x - 4}}{{\text{x}}^2}$
On simplifying, we get
$ \Rightarrow $ Area of gravel path=$176 - 4{{\text{x}}^2}$ sq.m.
Now, the cost of laying flower bed=area of flower bed × rate per sq. m. and we can write rate as$2.75 = \dfrac{{275}}{{100}}$ .Then on putting the values, we get-
$ \Rightarrow $ The cost of laying flower bed=${\left( {44 - 2{\text{x}}} \right)^2} \times \dfrac{{275}}{{100}} = \dfrac{{11}}{4}{\left( {44 - 2{\text{x}}} \right)^2} = 11{\left( {22 - {\text{x}}} \right)^2}$
And the cost of laying gravel path=area of gravel path × rate per sq. m. We can write rate as$1.50 = \dfrac{{150}}{{100}}$ .Then on putting values, we get-
$ \Rightarrow $ Cost of laying gravel path=$\left( {176 - 4{{\text{x}}^2}} \right)\dfrac{{150}}{{100}} = 6\left( {44 - {{\text{x}}^2}} \right) = 264 - 6{{\text{x}}^2}$
According to the question we know that the total cost of laying flower bed and gravel path=$4904$ Rs.
So,$ \Rightarrow 11{\left( {22 - {\text{x}}} \right)^2} + 264 - 6{{\text{x}}^2} = 4904$
On solving the eq. we get,
$
   \Rightarrow 11\left( {484 + {{\text{x}}^2} - 44{\text{x}}} \right) + 264 - 6{{\text{x}}^2} = 4904 \\
   \Rightarrow 5324 + 11{{\text{x}}^2} - 484{\text{x + }}264 - 6{{\text{x}}^2} = 4904 \\
   \Rightarrow 5{{\text{x}}^2} - 220{\text{x + 5324 = 4904}} \\
   \Rightarrow 5{{\text{x}}^2} - 220{\text{x + 420 = 0}} \\
 $
On dividing the eq. by 5, we get-
$ \Rightarrow {{\text{x}}^2} - 44{\text{x + 84 = 0}}$
By factoring, we get-
\[
   \Rightarrow {{\text{x}}^2} - 42{\text{x - 2x + 84 = 0}} \\
   \Rightarrow {\text{x}}\left( {{\text{x - 42}}} \right) - 2\left( {{\text{x - 42}}} \right) = 0 \\
   \Rightarrow \left( {{\text{x - 42}}} \right)\left( {{\text{x - 2}}} \right) = 0 \\
   \Rightarrow {\text{x = 42 or x = 2}} \\
 \]
But since the side of the square field =$44$ m so the width of gravel path cannot be longer than that.
So the width of gravel path =$2{\text{m}}$.

Note: Here, the student may go wrong when calculating the side of the flower bed assuming it to be \[44 - {\text{x}}\] which is wrong because the gravel path covers $2{\text{x m}}$ of the side of the square field so each side of flower bed=$\left( {44 - 2{\text{x}}} \right)$ m