Question

There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks and in the line with the tree. If the angle of elevation of the top of the tree from P and Q are respectively ${30^ \circ }$ and ${45^ \circ }$. Find the height of the tree.

Answer 1

Hint:
We will begin by drawing 2 right triangles. From the two triangles, find the trigonometric ratios involving the height of the tree and the distance from its base to the point. Then, solve the equations to find the height of the tree.

Complete step by step solution:
According to the given statement, we have the condition as shown in the figure below.

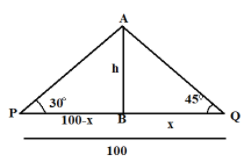
There are two points P an Q and the distance between them be 100m
Let $AB = h$ be the height of the tree.
Let the distance from the base of the tree $B$ to the point Q be $x$, then the distance from point P to the base of tree will be $100 - x$
Consider triangle, $ABQ$
$\tan {45^ \circ } = \dfrac{{AB}}{{BQ}}$
We know that $\tan {45^ \circ } = 1$
On substituting the known values, we will get,
$
   \Rightarrow 1 = \dfrac{h}{x} \\
   \Rightarrow x = h \\
$
Consider triangle $ABP$
$\tan {30^ \circ } = \dfrac{h}{{100 - x}}$
We know that $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ and $x = h$
On substituting the known values, we will get,
$
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{100 - h}} \\
   \Rightarrow 100 - h = h\sqrt 3 \\
   \Rightarrow h\left( {\sqrt 3 + 1} \right) = 100 \\
$
Divide both sides by \[\left( {\sqrt 3 + 1} \right)\]
$h = \dfrac{{100}}{{\sqrt 3 + 1}}$

Hence, the height of the tree is $\dfrac{{100}}{{\sqrt 3 + 1}}$ metres.

Note:
In these types of questions, diagrams play an important role as it helps to understand the question in a better way. Students must know all the trigonometric ratios for this type of question. here, we have used tangent ratio and $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$