Question

There is a rod of length \[l\] and mass \[m\]. It is hinged at one end to the ceiling. Find the period of small oscillation.
A. \[T = 2\pi \sqrt {\left( {\dfrac{{2l}}{{3g}}} \right)} \]
B. \[T = \pi \sqrt {\left( {\dfrac{l}{{3g}}} \right)} \]
C. \[T = 2\pi \sqrt {\left( {\dfrac{l}{{3g}}} \right)} \]
D. \[T = 2\pi \sqrt {\left( {\dfrac{l}{g}} \right)} \]

Answer 1

Hint: Use the formulae for the torque, angular acceleration, moment of inertia of the rod about one of its ends, angular acceleration and the period of an object. Start from the torque due to the weight of the rod. Use the condition in terms of torque for the oscillation of the rod.

Formula used:
The torque \[\tau \] due to a force \[F\] is given by
\[\tau = Fr\sin \theta \] …… (1)

Here, is the distance between the force and the centre around which the object moves and \[\theta \] is the angle between the force and the distance.

The moment of inertia \[I\] of a rod about one of its ends is
\[I = \dfrac{{m{l^2}}}{3}\] …… (2)

Here, \[m\] is the mass of the rod and \[l\] is the length of the rod.

The torque \[\tau \] on an oscillating or rotating body is given by
\[\tau = I\alpha \] …… (3)

Here, \[I\] is the moment of inertia of the body and \[\alpha \] is the angular acceleration of the body.

The angular acceleration \[\alpha \] of an oscillating object is
\[\alpha = - {\omega ^2}\theta \] …… (4)

Here, \[\omega \] is the angular velocity of the object and \[\theta \] is the angular displacement of the object.

The time period \[T\] of an object is given by
\[T = \dfrac{{2\pi }}{\omega }\] …… (5)

Here, \[\omega \] is the angular velocity of the object.

Complete step by step answer:
A rod of mass \[m\] and length \[l\] is hinged at its one end to the ceiling.

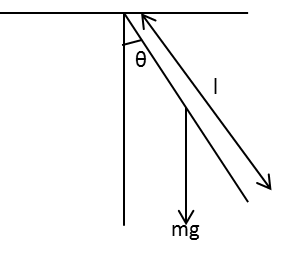
The rod is hinged at the ceiling performs small oscillations with a small angle \[\theta \].

\[mg\] is the weight of the rod acting in the downward direction at the centre of the rod.

Determine the torque \[\tau \] acting on the rod due to the weight of the rod.

Substitute \[mg\] for \[F\] and \[\dfrac{l}{2}\] for \[r\] in equation (1).
\[\tau = - mg\dfrac{l}{2}\sin \theta \]

Since the angle \[\theta \] is very small for small oscillations, \[\sin \theta \approx \theta \]
\[\tau = - \dfrac{{mgl}}{2}\theta \]

The above equation resembles the condition for the oscillating body that the torque \[\tau \] on the oscillating body is directly proportional to the angular displacement \[\theta \] of the body and opposes the oscillation of the body.
\[\tau \propto - \theta \]
\[ \Rightarrow \tau = - c\theta \] …… (6)

Therefore, it can be concluded from the above equations that
\[c = \dfrac{{mgl}}{2}\]

Substitute for \[\tau \] in the above equation (6).
\[I\alpha = - c\theta \]
\[ \Rightarrow \alpha = \dfrac{{ - c\theta }}{I}\]

Substitute \[ - {\omega ^2}\theta \] for \[\alpha \] in the above equation.
\[ - {\omega ^2}\theta = \dfrac{{ - c\theta }}{I}\]
\[{\omega ^2} = \dfrac{c}{I}\]
\[\omega = \sqrt {\dfrac{c}{I}} \]

Determine the period of small oscillation of the rod.

Substitute \[\sqrt {\dfrac{c}{I}} \] for \[\omega \] in equation (5).
\[T = \dfrac{{2\pi }}{{\sqrt {\dfrac{c}{I}} }}\]
\[ \Rightarrow T = 2\pi \sqrt {\dfrac{I}{c}} \]

Substitute \[\dfrac{{m{l^2}}}{3}\] for \[I\] and \[\dfrac{{mgl}}{2}\] for \[c\] in the above equation.
\[T = 2\pi \sqrt {\dfrac{{\dfrac{{m{l^2}}}{3}}}{{\dfrac{{mgl}}{2}}}} \]
\[ \Rightarrow T = 2\pi \sqrt {\dfrac{{2l}}{{3g}}} \]

Therefore, the period of oscillation of the rod is \[2\pi \sqrt {\dfrac{{2l}}{{3g}}} \].

So, the correct answer is “Option A”.

Note:
The torque due to the weight of the rod is negative because the direction of the torque is clockwise.
The rod is hinged at the ceiling performs small oscillations with a small angle \[\theta \].