
There are two candidates in an election 11% of the voters did not vote. 500 votes were declared invalid. The elected candidate 3300 votes more than his opponents. If the elected candidate got 48% of the total votes, how many votes did each candidate get?
Answer
581.4k+ views
Hint: As we know, 2 candidates are there and if we assume the total votes is 100% then out of this 100%, 11% are non-voters, Also, 500 voters declared invalid. And the candidates who got elected have 3300 more votes than opponents. And here also mentioned that only 48% of total votes gain by elected candidates.
Complete step by step solution:
Let voters are 100%, then,
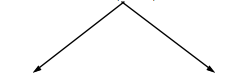
11% (did not vote) 89% (given vote)
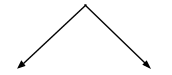
500 (votes are invalid) 89% - 500 (votes are valid)
Elected candidate got 48% of total vote then loser candidate got (89% - 500 – 48%)
89% - 500 (votes are valid)

48% (winner candidate) (89% - 500 – 48%) loser candidate
Elected candidate got 3300 votes more than his opponent.
$\therefore $ winner candidate – loser candidate = 3300
48% -( 89%-500-48%) = 3300
48% -( 41%-500)= 3300
48% - 41%+500 =3300
7% = 2800
1% = 400
100% = 40000
Total voters (votes) = 40000
Winner candidate = 40000 $\times \dfrac{{48}}{{100}}$ = 19200 votes.
Loser candidate = 19200 – 3300 = 15900 votes.
Therefore, the required value is (19200) & (15900) votes.
Note: first to take votes (total) is 100% then process the question winner candidate is 48% of total votes and loser candidate gets 3300 votes less than winner candidate.
Complete step by step solution:
Let voters are 100%, then,
100% (voters)

11% (did not vote) 89% (given vote)

500 (votes are invalid) 89% - 500 (votes are valid)
Elected candidate got 48% of total vote then loser candidate got (89% - 500 – 48%)
89% - 500 (votes are valid)

48% (winner candidate) (89% - 500 – 48%) loser candidate
Elected candidate got 3300 votes more than his opponent.
$\therefore $ winner candidate – loser candidate = 3300
48% -( 89%-500-48%) = 3300
48% -( 41%-500)= 3300
48% - 41%+500 =3300
7% = 2800
1% = 400
100% = 40000
Total voters (votes) = 40000
Winner candidate = 40000 $\times \dfrac{{48}}{{100}}$ = 19200 votes.
Loser candidate = 19200 – 3300 = 15900 votes.
Therefore, the required value is (19200) & (15900) votes.
Note: first to take votes (total) is 100% then process the question winner candidate is 48% of total votes and loser candidate gets 3300 votes less than winner candidate.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Name the states through which the Tropic of Cancer class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE




