Question

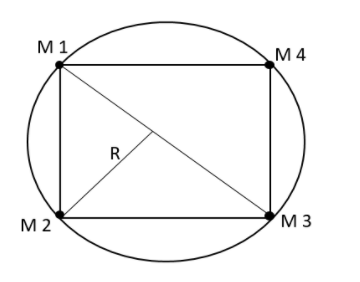
There are four particles, each of the mass $M$ in the action of their mutual gravitational attraction, along a circle of radius $R$. What will be the speed of each particle?
$\begin{align}
  & A.\dfrac{GM}{R} \\
 & B.\sqrt{2\sqrt{2}\dfrac{GM}{R}} \\
 & C.\sqrt{\dfrac{GM}{R}\left( 2\sqrt{2}+1 \right)} \\
 & D.\sqrt{\dfrac{GM}{R}\left( \dfrac{2\sqrt{2}+1}{4} \right)} \\
\end{align}$

Answer 1

Hint: Gravitational forces between two masses can be found by taking the product of the gravitational constant, mass of the first particle and the mass of the second particle to the distance between the bodies which is squared. Equate this resultant force with the centripetal force. The centripetal force can be found by taking the ratio of the product of the mass and the square of the velocity to the radius of the circular path. This will help you in answering this question.

Complete step by step answer:
Gravitational forces between two masses can be found by taking the product of the gravitational constant, mass of the first particle and the mass of the second particle to the distance between the bodies which is squared. That is we can write that,
$F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{d}^{2}}}$
Therefore the force between the first and the second particle and the force between the first and the fourth particle will be equivalent. That is we can write that,
${{F}_{12}}={{F}_{14}}=\dfrac{GM}{2{{R}^{2}}}$
The resultant of these two forces can be shown as,
$\dfrac{\sqrt{2}G{{M}^{2}}}{2{{R}^{2}}}$
Therefore the force between the first and the third particle can be shown as,
${{F}_{13}}=\dfrac{G{{M}^{2}}}{4{{R}^{2}}}$
Therefore the combined resultant of these two forces can be shown as,
\[{{F}_{net}}=\dfrac{\sqrt{2}G{{M}^{2}}}{2{{R}^{2}}}+\dfrac{G{{M}^{2}}}{4{{R}^{2}}}\]
Simplifying this equation can be shown as,
\[{{F}_{net}}=\dfrac{G{{M}^{2}}}{{{R}^{2}}}\left[ \dfrac{\sqrt{2}}{2}+\dfrac{1}{4} \right]\]
Now let us equate this resultant force with the centripetal force. The centripetal force can be found by taking the ratio of the product of the mass and the square of the velocity to the radius of the circular path. Therefore we can write that,
\[\dfrac{M{{v}^{2}}}{R}=\dfrac{G{{M}^{2}}}{{{R}^{2}}}\left[ \dfrac{2\sqrt{2}+1}{4} \right]\]
Rearranging this equation can be written as,
\[{{v}^{2}}=\dfrac{GM}{R}\left[ \dfrac{2\sqrt{2}+1}{4} \right]\]
Taking the square root of this,
\[v=\sqrt{\dfrac{GM}{R}\left[ \dfrac{2\sqrt{2}+1}{4} \right]}\]
Therefore the speed of the particle has been calculated.

Note: The gravitational force can be defined as a force which will attract any two bodies with mass. We can describe the gravitational force attractive as it will always try to pull masses together, it will never push them apart. The force of gravity has been expressed in the units of newton.