Question

There are \[8\] different types of tyres in a store, each in both tube and tubeless variety, each with either nylon on rayon cards and each with white sidewalls or plain black. How many different kinds of tyres are there?

Answer 1

Hint:For this type of question, we need to draw different types of tyres. Therefore we can understand how many tyres present there. we can solve the problem by permutations and combinations. In this way, we can find the no of tyres pressed there.


Complete step by step solution:
So let’s see the tree I have drawn. This figure shows the arrangement of tyres. By this way, we can find the classification of tyres.

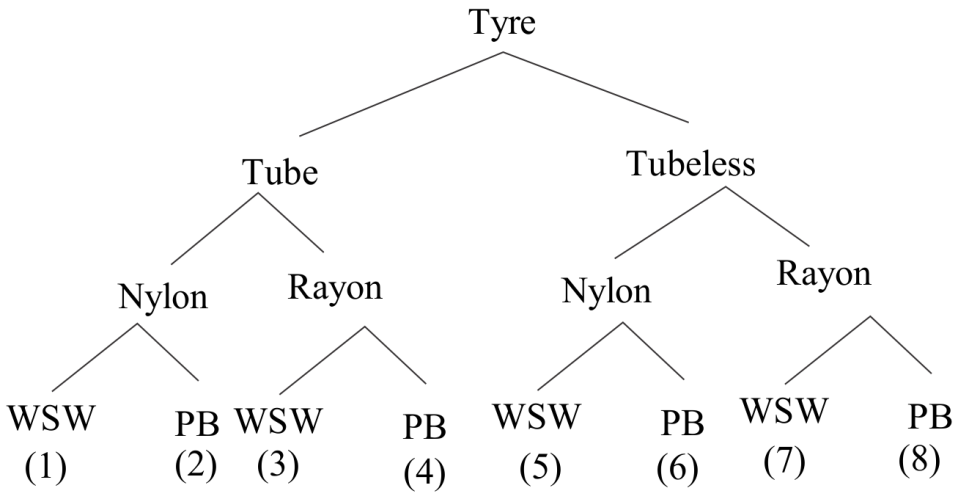
Total no of tyres is
$ = 8 \times 8 = 64{\text{ Tyres}}{\text{.}}$
Arrange in
\[\left( 1 \right)\]Size
\[\left( 2 \right)\]Tube or Tubeless
\[\left( 3 \right)\] Nylon or Rayon
\[\left( 4 \right)\]Sidewalls units in black ways.
So arrangement will be-
$\begin{gathered}
  ^O{C_1}{ \times ^2}{C_1}{ \times ^4}{C_1}{ \times ^8}{C_1} \\
   = 8 \times 4 \times 2 \times 8 \\
   = 512 \\
\end{gathered} $
Total different kinds of tyres.
$\begin{gathered}
   = 512 \times 8 \\
   = 4176 \\
\end{gathered} $


Note: Permutation & combination makes calculations easier. In this method we can find the total no of arrangement and how many kinds of such arrangement. so this is the simplest way to get the results.Do not get confused and apply combinations here