Answer
357.7k+ views
Hint:Given that students are standing in such a manner that number of rows and number of columns are equal in a P.T. drill. Then, first break the number (of students) as the product of its factors and then make pairs of numbers. The numbers left in the product whose pairs are not possible, will be the number of students left out in this arrangement.
Complete step-by-step answer:
Number of students in the school = 500
500 can be written as
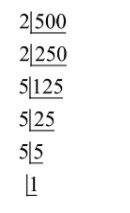
i.e., $500 = 2 \times 2 \times 5 \times 5 \times 5$
$ \Rightarrow \sqrt {500} = \sqrt {2 \times 2 \times 5 \times 5 \times 5} = 10\sqrt 5 = 10 \times 2.03 = 22.03 \approx 22$
$ \Rightarrow $In each row or each column maximum 22 students can be arranged
$ \Rightarrow $maximum students can participate in P.T. drill will ${\left( {22} \right)^2}$
Therefore, the number of students left out$ = 500 - {\left( {22} \right)^2} = 500 - 484 = 16$.
Note:The question can also be done by assuming that
Number of students in rows be x and number of students in columns are in the same number x.
Then, $x \times x = 500 \Rightarrow x = \sqrt {500} $
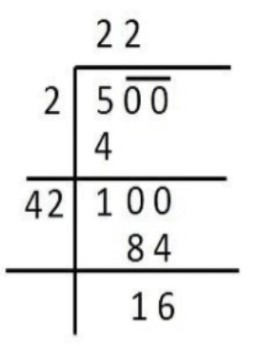
Here the remainder is 16, which is the number of students left out.
The H.C.F. defines the greatest factor present in between given two or more numbers, whereas L.C.M. defines the least number which is exactly divisible by two or more numbers. H.C.F. is also called the greatest common factor (GCF) and LCM is also called the Least Common Divisor.
Complete step-by-step answer:
Number of students in the school = 500
500 can be written as
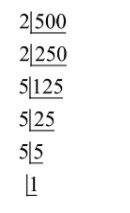
i.e., $500 = 2 \times 2 \times 5 \times 5 \times 5$
$ \Rightarrow \sqrt {500} = \sqrt {2 \times 2 \times 5 \times 5 \times 5} = 10\sqrt 5 = 10 \times 2.03 = 22.03 \approx 22$
$ \Rightarrow $In each row or each column maximum 22 students can be arranged
$ \Rightarrow $maximum students can participate in P.T. drill will ${\left( {22} \right)^2}$
Therefore, the number of students left out$ = 500 - {\left( {22} \right)^2} = 500 - 484 = 16$.
Note:The question can also be done by assuming that
Number of students in rows be x and number of students in columns are in the same number x.
Then, $x \times x = 500 \Rightarrow x = \sqrt {500} $

Here the remainder is 16, which is the number of students left out.
The H.C.F. defines the greatest factor present in between given two or more numbers, whereas L.C.M. defines the least number which is exactly divisible by two or more numbers. H.C.F. is also called the greatest common factor (GCF) and LCM is also called the Least Common Divisor.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Why Are Noble Gases NonReactive class 11 chemistry CBSE

Let X and Y be the sets of all positive divisors of class 11 maths CBSE

Let x and y be 2 real numbers which satisfy the equations class 11 maths CBSE

Let x 4log 2sqrt 9k 1 + 7 and y dfrac132log 2sqrt5 class 11 maths CBSE

Let x22ax+b20 and x22bx+a20 be two equations Then the class 11 maths CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

Write a letter to the principal requesting him to grant class 10 english CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Fill in the blanks A 1 lakh ten thousand B 1 million class 9 maths CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Difference Between Plant Cell and Animal Cell

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE



