Question

There are \[50\] circular plates each of radius \[7\,cm\] and thickness \[\dfrac{1}{2}\,cm\] are placed one above another to form a solid right circular cylinder . Find total surface area and volume of the cylinder so formed.

Answer 1

Hint:In the given questions , the height of the cylinder can be obtained by adding the thickness of each of the \[50\] circular plates . To find the volume of formed cylinder we use the formula \[ = \pi {r^2}h\] and for the surface area of the cylinder formed is given by \[ = 2\pi r\left( {r + h} \right)\] , where \[r\] is the radius of the circular disc and \[h\] is the height of formed cylinder .

Complete step by step answer:
Number of plates \[ = 50\]
Radius of the given plates \[ = 7cm\]
Height of the cylinder formed by the plates \[ = \left( {\dfrac{1}{2} \times 50} \right)cm\]

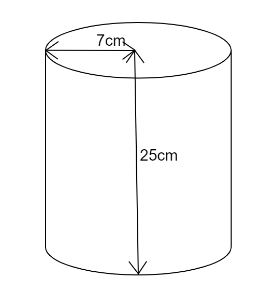
On solving we get, height of the cylinder \[ = 25cm\]. Now we will find the surface area of the cylinder formed using the formula \[S = 2\pi r\left( {r + h} \right)\] .
On putting the values in the formula we get ,
\[S = 2\pi \times 7 \times \left( {7 + 25} \right)c{m^2}\]
On simplifying we get ,
\[S = 2\pi \times 7 \times \left( {33} \right)c{m^2}\]
On solving we get ,
\[S = \left( {2\pi \times 231} \right)c{m^2}\]
Putting value of \[\pi = \dfrac{{22}}{7}\] , we get
\[S = \left( {2 \times \dfrac{{22}}{7} \times 231} \right)c{m^2}\]
On solving we get ,
\[S = \left( {\dfrac{{10164}}{7}} \right)c{m^2}\]
On solving we get ,
\[\therefore S = 1452\,c{m^2}\]

Now for the volume of the formed cylinder , we will use the formula \[V = \pi {r^2}h\]
On putting the values we get ,
\[V = \left[ {\pi \times {{\left( 7 \right)}^2} \times 25} \right]c{m^3}\]
On simplifying we get ,
\[V = \left( {\pi \times 49 \times 25} \right)c{m^3}\]
Now putting \[\pi = \dfrac{{22}}{7}\] we get ,
\[V = \left( {\dfrac{{22}}{7} \times 49 \times 25} \right)c{m^3}\]
On solving we get ,
\[V = \left( {22 \times 7 \times 25} \right)c{m^3}\]
On solving further we get ,
\[\therefore V = 3850\,c{m^3}\]

Therefore , the surface area of the formed cylinder is \[1452\,c{m^2}\] and the volume of the formed cylinder is \[3850\,c{m^3}\].

Note:The height of the cylinder should not be taken as the thickness of the individual disc as , there are \[50\] discs so add the thickness of each of the \[50\] discs to get the required height of the cylinder . Do not use the value of \[\pi \] as \[\pi = 3.14\] , as it will complicate the solution . Always remember to put the unit of the dimensions as provided in the question.