Question

The $y = 2$ is a line
A. Parallel to x-axis
B. Parallel to y-axis
C. Passing through origin
D. None

Answer 1

Hint: In order to find the state of a line for the given equation, initiate with thinking out the possible properties of the line, what are the coordinates that it covers. Then draw the graph of the equation using the conditions and check out at what position it lies.

Complete step by step answer:
We are given with an equation $y = 2$. We know that there are two values in a $\left( {x,y} \right)$ coordinate that is x-value and the y-value. Since, the value of y is given to us is a constant term, and the value of x coordinate is not given. This means whatever we place the value of x, the value of y will always be the same , that is $y = 2$.

For example, we take $x = 0$, we have $y = 2$, so the point becomes $\left( {0,2} \right)$.Similarly, when we take $x = 4$, we have $y = 2$, so the point becomes $\left( {4,2} \right)$.And, when we take $x = - 3$, we have $y = 2$, so the point becomes $\left( { - 3,2} \right)$.Substituting all these points on the graph and joining them we get:

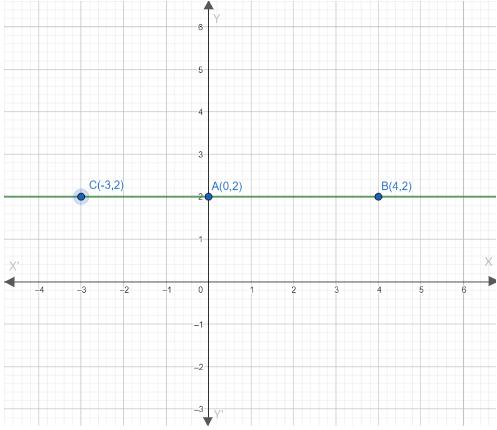
And, we can see that the line becomes parallel to the x-axis. Therefore, $y = 2$ is a line that is Parallel to the x-axis.

Hence, option A is correct.

Note: It has already been proved that in general if $x = a$, then the line will be parallel to y-axis and if $y = b$, then the line will be parallel to x-axis, where a and b are any constant terms. It’s important to graph the values by taking some general points in order to make an equation of a line.