
The work done on a particle of mass m by a force $K\left[ {\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop j\limits^ \wedge } \right]$ (K being the constant of appropriate dimensions, when the particle is taken from the point (a, 0) to the point (0, a) along a circular path of radius a about the origin in the x-y plane is:
A. $\dfrac{{2Kx}}{a}$
B. $\dfrac{{Kx}}{a}$
C. $\dfrac{{Kx}}{{2a}}$
D. 0
Answer
584.7k+ views
Hint: Work done on a particle by force is the dot product of the force and the displacement. Hence work done is not a vector and it is a scalar quantity. If force and displacement are perpendicular to each other then the work done will be zero as dot product between them will become zero.
Formula used: ${x^2} + {y^2} = {r^2}$
Complete step by step answer:
To denote the position of a point on a coordinate system from the origin we denote it by using a vector notation. If x-coordinate is x and y-coordinate is y then the vector notation to denote that point is $x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge $. Now the unit vector of this vector gives us the direction of this vector. The property of unit vectors is that even if we multiply the unit vector with any magnitude the direction will remain the same but only magnitude changes.
The equation of the circle which has origin as its center and ‘r’ as radius is ${x^2} + {y^2} = {r^2}$
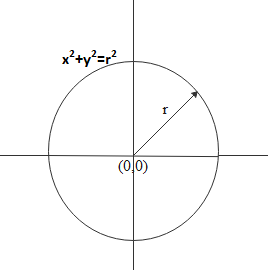
Magnitude of that radius will be
$\left| r \right| = {({x^2} + {y^2})^{\dfrac{1}{2}}}$
Now for the vector $x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge $ its unit vector will be $\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{1}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{1}{2}}}}}\mathop j\limits^ \wedge = \dfrac{x}{{\left| r \right|}}\mathop i\limits^ \wedge + \dfrac{y}{{\left| r \right|}}\mathop j\limits^ \wedge = \dfrac{1}{{\left| r \right|}}(x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge ) = \mathop r\limits^ \wedge $
We have the force equation $K\left[ {\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop j\limits^ \wedge } \right]$
If there is an expression ${p^{\dfrac{a}{b}}}$ we can write it as ${\left( {{p^{\dfrac{1}{b}}}} \right)^a}$
So ${p^{\dfrac{a}{b}}} = {\left( {{p^{\dfrac{1}{b}}}} \right)^a}$ in the same way we will write ${({x^2} + {y^2})^{\dfrac{3}{2}}}$ as ${\left[ {{{({x^2} + {y^2})}^{\dfrac{1}{2}}}} \right]^3}$ because we will convert this expression in terms of magnitude of the radial vector.
$\eqalign{
& {({x^2} + {y^2})^{\dfrac{3}{2}}} = {\left[ {{{({x^2} + {y^2})}^{\dfrac{1}{2}}}} \right]^3} \cr
& \Rightarrow {({x^2} + {y^2})^{\dfrac{3}{2}}} = {\left[ {\left| r \right|} \right]^3} \cr} $
By substituting the above result in force equation we have
$F = K\left[ {\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop j\limits^ \wedge } \right]$=$K\left[ {\dfrac{x}{{{{\left| r \right|}^3}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{\left| r \right|}^3}}}\mathop j\limits^ \wedge } \right] = \dfrac{K}{{{{\left| r \right|}^2}}}\left[ {\dfrac{x}{{\left| r \right|}}\mathop i\limits^ \wedge + \dfrac{y}{{\left| r \right|}}\mathop j\limits^ \wedge } \right] = \dfrac{K}{{{{\left| r \right|}^2}}}\mathop r\limits^ \wedge $ because $\dfrac{1}{{\left| r \right|}}(x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge ) = \mathop r\limits^ \wedge $
We had converted the force equation in the form of magnitude of the radial vector I.e $\left| r \right|$ and found out the direction of force in terms of radial vector direction i.e $\mathop r\limits^ \wedge $ .
From the above equation it is clearly evident that the force is along the radius i.e along the radial direction. This will be perpendicular to the tangent to the circle i.e displacement and hence the dot product of force and displacement will be zero.
So, the correct answer is “Option D”.
Note: This can be interpreted like the particle is executing the circular motion along the circle and the force is action radial to it i.e can be assumed as the kind of centrifugal force and hence work done by that force is zero. It can also be solved by using the method of integration which will become very lengthy and requires the tricks to solve the integrals.
Formula used: ${x^2} + {y^2} = {r^2}$
Complete step by step answer:
To denote the position of a point on a coordinate system from the origin we denote it by using a vector notation. If x-coordinate is x and y-coordinate is y then the vector notation to denote that point is $x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge $. Now the unit vector of this vector gives us the direction of this vector. The property of unit vectors is that even if we multiply the unit vector with any magnitude the direction will remain the same but only magnitude changes.
The equation of the circle which has origin as its center and ‘r’ as radius is ${x^2} + {y^2} = {r^2}$
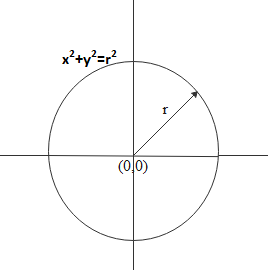
Magnitude of that radius will be
$\left| r \right| = {({x^2} + {y^2})^{\dfrac{1}{2}}}$
Now for the vector $x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge $ its unit vector will be $\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{1}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{1}{2}}}}}\mathop j\limits^ \wedge = \dfrac{x}{{\left| r \right|}}\mathop i\limits^ \wedge + \dfrac{y}{{\left| r \right|}}\mathop j\limits^ \wedge = \dfrac{1}{{\left| r \right|}}(x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge ) = \mathop r\limits^ \wedge $
We have the force equation $K\left[ {\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop j\limits^ \wedge } \right]$
If there is an expression ${p^{\dfrac{a}{b}}}$ we can write it as ${\left( {{p^{\dfrac{1}{b}}}} \right)^a}$
So ${p^{\dfrac{a}{b}}} = {\left( {{p^{\dfrac{1}{b}}}} \right)^a}$ in the same way we will write ${({x^2} + {y^2})^{\dfrac{3}{2}}}$ as ${\left[ {{{({x^2} + {y^2})}^{\dfrac{1}{2}}}} \right]^3}$ because we will convert this expression in terms of magnitude of the radial vector.
$\eqalign{
& {({x^2} + {y^2})^{\dfrac{3}{2}}} = {\left[ {{{({x^2} + {y^2})}^{\dfrac{1}{2}}}} \right]^3} \cr
& \Rightarrow {({x^2} + {y^2})^{\dfrac{3}{2}}} = {\left[ {\left| r \right|} \right]^3} \cr} $
By substituting the above result in force equation we have
$F = K\left[ {\dfrac{x}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{({x^2} + {y^2})}^{\dfrac{3}{2}}}}}\mathop j\limits^ \wedge } \right]$=$K\left[ {\dfrac{x}{{{{\left| r \right|}^3}}}\mathop i\limits^ \wedge + \dfrac{y}{{{{\left| r \right|}^3}}}\mathop j\limits^ \wedge } \right] = \dfrac{K}{{{{\left| r \right|}^2}}}\left[ {\dfrac{x}{{\left| r \right|}}\mathop i\limits^ \wedge + \dfrac{y}{{\left| r \right|}}\mathop j\limits^ \wedge } \right] = \dfrac{K}{{{{\left| r \right|}^2}}}\mathop r\limits^ \wedge $ because $\dfrac{1}{{\left| r \right|}}(x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge ) = \mathop r\limits^ \wedge $
We had converted the force equation in the form of magnitude of the radial vector I.e $\left| r \right|$ and found out the direction of force in terms of radial vector direction i.e $\mathop r\limits^ \wedge $ .
From the above equation it is clearly evident that the force is along the radius i.e along the radial direction. This will be perpendicular to the tangent to the circle i.e displacement and hence the dot product of force and displacement will be zero.
So, the correct answer is “Option D”.
Note: This can be interpreted like the particle is executing the circular motion along the circle and the force is action radial to it i.e can be assumed as the kind of centrifugal force and hence work done by that force is zero. It can also be solved by using the method of integration which will become very lengthy and requires the tricks to solve the integrals.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




