Question

The wheel shown in the diagram has a fixed axle passing through O. The wheel is kept stationary under the action of

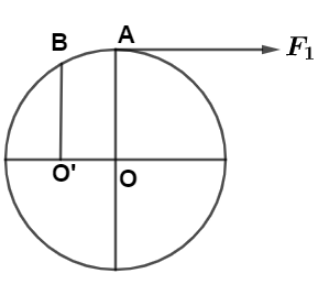
(i) Horizontal force ${F_1}$ at A and
(ii) A vertical force ${F_2}$ at B.
Show the direction of force ${F_2}$ in the diagram.

Answer 1

Hint:In order to solve this question we need to understand torque. Torque is defined as a rotating force which causes different bodies to rotate. It is mathematically defined as the cross product of force and the perpendicular distance from the axis to the line of action of force. It is a vector quantity and direction of rotation of circular bodies can be found using cross product rule, which states that for direction stretch your palm in direction of first vector and rotate fingers in direction of second vector, so the thumb direction is torque direction.

Complete step by step answer:
Since in figure, a horizontal force ${F_1}$ acts at A, so for torque direction we draw a perpendicular from axle point O to A whose distance is equal to radius and this vector points in upward direction, so torque due to ${F_1}$ is given by,
\[{\vec \tau _1} = \vec r \times {\vec F_1}\]
Since $\vec r$ is perpendicular to ${\vec F_1}$ so torque become,
\[{\vec \tau _1} = \left| {\vec r} \right|\left| {{{\vec F}_1}} \right|( - \hat n)\]
Here, the negative sign denotes the torque due to ${F_1}$ being into the plane of paper.
For wheel to stationary, there must be torque in outward direction,

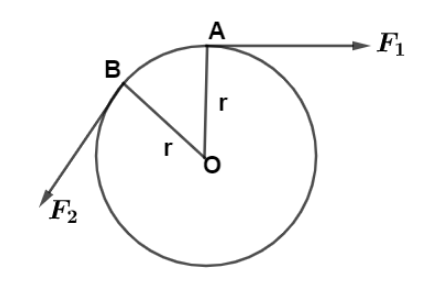
Consider a force ${F_2}$ which in direction as shown, now for torque we draw a perpendicular from axle point O to B whose distance is equal to radius and this vector points in upward direction, so torque due to ${F_2}$ is given by,
\[{\vec \tau _2} = \vec r \times {\vec F_2}\]
Since $\vec r$ is perpendicular to ${\vec F_2}$ so torque become,
\[{\vec \tau _2} = \left| {\vec r} \right|\left| {{{\vec F}_2}} \right|( + \hat n)\]
Here, the positive sign denotes the torque due to ${F_2}$ being out of the plane of paper.

So in this way net torque is zero, and hence the wheel is stationary, so it cannot rotate.

Note: It should be remembered that here we have assumed that there would be no translation motion and also there would be no friction means the wheel is kept at a smooth surface. Also we assumed that the point of contact of the wheel is at rest and since there is no translation motion, the wheel could not drag itself. Also the direction of torque is determined using the cross product direction rule.