Question

The wavelength of green light from a traffic signal is about 520nm. Calculate the frequency and wave number of this radiation.

Answer 1

Hint: We know that the universal constant c, the speed of light in vacuum, is given by the product of light’s frequency and wavelength and also that the wave number as the reciprocal of wavelength. So we could apply the above two points to find the solution to the given question.

Formula used:
$c=\nu \lambda $
$\overline{\nu }=\dfrac{1}{\lambda }$

Complete answer:
From our previous knowledge on light, we know that it is an electromagnetic radiation that shows wave nature. Light being a wave is known to have frequency, amplitude, wavelength and wavenumber.

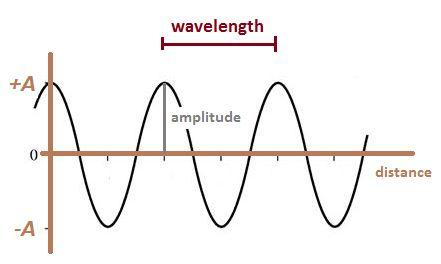
Now let us define each one of them.

Wavelength: It can be defined as the distance between corresponding points in two adjacent light cycles. It is normally represented by ‘$\lambda $’. It has units of lengths.

Frequency: It can be defined as the number of cycles of light that pass a given point in one second. It is represented by Greek letter ‘$\nu $’. It is also the reciprocal of time period and has the unit ‘${{s}^{-1}}$’ but normally we use (Hz) as its unit.

Amplitude: It can be defined as the magnitude of a wave’s displacement or simply as half the height of the wave from consecutive crust and trough.

Wave number: It can be defined as the number of waves per unit distance or simply as spatial frequency of a wave. It is represented by $\overline{\nu }$ .

Now that we have defined every term, let us discuss the relationship between them.
Speed of any wave v is given by the product of its wavelength and its frequency, that is,
Speed v $=\nu \lambda $
But we know speed of light travelling in vacuum is a universal constant represented by ‘c’ and has the value of $c=3\times {{10}^{8}}m{{s}^{-1}}$ .
So now we could give the relation between $c$, $\nu $ and $\lambda $ as,
$c=\nu \lambda $ ………………….. (1)
Wavelength $\lambda $ in this question is given as 520nm, that is,
$\lambda =520\times {{10}^{-9}}nm$ …………… (2)
Substituting (2) in equation (1) gives,
$\nu =\dfrac{c}{\lambda }=\dfrac{3\times {{10}^{8}}}{520\times {{10}^{-9}}}Hz$
Therefore, we get frequency $\nu $ as,
$\nu =5.77\times {{10}^{14}}Hz$ .
Wave number by definition is the reciprocal of wavelength, that is,
$\overline{\nu }=\dfrac{1}{\lambda }$
$\overline{\nu }=\dfrac{1}{520nm}$
$\overline{\nu }=1.92\times {{10}^{-3}}n{{m}^{-1}}$ .
Therefore, we get frequency $\nu =5.77\times {{10}^{14}}Hz$ and wave number $\overline{\nu }=1.92\times {{10}^{-3}}n{{m}^{-1}}$ as the solutions to the given question.

Note:
While finding the frequency of the light, you should make sure that you convert the given value of wavelength in its SI unit, that is, meters. But we can see that this is not compulsory in the case of wave numbers as it can be expressed as the inverse of the wavelength's unit.