Question

The volume of metallic cylindrical pipe is $748c{{m}^{3}}$. Its length is 14cm and its external radius is 9cm. Find its thickness.
a. 1cm
b. 2cm
c. 4cm
d. 3cm

Answer 1

Hint: We will use the formula of volume of the cylindrical pipe, that is, $\pi h\left( {{R}^{2}}-{{r}^{2}} \right)$, where h is the height of the cylindrical pipe, R is the external radius and r is the internal radius of the cylindrical pipe. From this formula, we will find the value of the internal radius, r. Then, we will subtract the internal radius from the external radius in order to get the thickness of the cylindrical pipe.

Complete step-by-step answer:
It is given in the question that the volume of metallic cylindrical pipe is $748c{{m}^{3}}$. Its length is 14cm and its external radius is 9cm. And we have been asked to find its thickness.
So, from the given data, we can say that the volume of the cylindrical pipe is $748c{{m}^{3}}$, the height of the cylindrical pipe is 14cm and the external radius, R is given as 9cm. Now, we will assume the value of the internal radius of the cylindrical pipe as ‘r’.
We can represent the cylindrical pipe as follows.

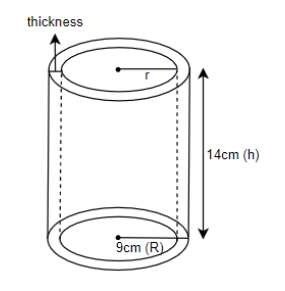
We know that the volume of the cylindrical pipe is given by, $\pi h\left( {{R}^{2}}-{{r}^{2}} \right)$, where h is the height of the cylindrical pipe, R is the external radius and r is the internal radius of the cylindrical pipe. So, we can write,
Volume of the cylindrical pipe = $\pi h\left( {{R}^{2}}-{{r}^{2}} \right)$
Now, on substituting the values of volume of the cylindrical pipe as 748, h as 14, R as 9 and $\pi =\dfrac{22}{7}$, in the above equation, we will get,
\[\begin{align}
  & 748=\dfrac{22}{7}\times 14\times \left( {{\left( 9 \right)}^{2}}-{{r}^{2}} \right) \\
 & 748=22\times 2\times \left( 81-{{r}^{2}} \right) \\
 & 748=44\left( 81-{{r}^{2}} \right) \\
\end{align}\]
On dividing the above equation by 44, we will get,
\[17=81-{{r}^{2}}\]
On transposing ${{r}^{2}}$ to the LHS and 17 to the RHS, we get,
\[\begin{align}
  & {{r}^{2}}=81-17 \\
 & {{r}^{2}}=64 \\
 & r=\sqrt{64} \\
 & r=8 \\
\end{align}\]
So, we get the internal radius of the cylindrical pipe as 8cm.
Now, we know that the thickness of the cylindrical pipe can be calculated as,
Thickness = (External radius of the cylindrical pipe) – (Internal radius of the cylindrical pipe)
= 9cm – 8cm
= 1cm
Therefore, we get the thickness of the cylindrical pipe as 1cm.
Hence, option (a) is the correct answer.

Note: Most of the students think that the thickness of the cylinder is the internal radius of the cylindrical pipe and hence, write the thickness of the cylindrical pipe as 8 cm, but it is wrong. So, the students must remember that the thickness of a cylindrical pipe is given by (external radius of the cylindrical pipe – internal radius of the cylindrical pipe). Also some students may make mistakes in the formula of volume and may write it as $\pi h\left( R-r \right)$ and forget to take the square of the R and r. The correct formula is $\pi h\left( {{R}^{2}}-{{r}^{2}} \right)$.