
The volume of cube is
Answer
499.5k+ views
Hint:For this we first let the side of a cube be ‘x’ and then form an equation using the mensuration volume formula of the cube and solving it to find the value of ‘x’ or required side of a cube.
Volume of a cube =
Complete step-by-step answer:
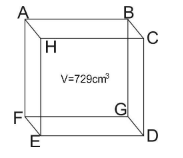
Let side of a cube = x m
Volume of given cube is =
But we know that the volume of a cube is given as
Therefore from above we have
Substituting value of volume in above formula, we have,
To find the cube root of a number
Prime factors of
Using prime factors. We have
Hence, from above we see that side a cube having volume
Note: Side of cube can be fide from given volume in two different way in first way we write given volume in term of exponent as
Volume of a cube =
Complete step-by-step answer:
Let side of a cube = x m
Volume of given cube is =
But we know that the volume of a cube is given as

Therefore from above we have
Substituting value of volume in above formula, we have,
To find the cube root of a number
Prime factors of
Using prime factors. We have
Hence, from above we see that side a cube having volume
Note: Side of cube can be fide from given volume in two different way in first way we write given volume in term of exponent as
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which of the following districts of Rajasthan borders class 9 social science CBSE

What is 85 of 500 class 9 maths CBSE

What is the full form of pH?

Define human made resources

India has states and Union Territories A 29 7 B 28 class 9 social science CBSE

What is the importance of natural resources? Why is it necessary to conserve them?




