Question

The volume of a sphere of radius $\pi cm$ is ______cc.
A. $\dfrac{4{{\pi }^{4}}}{3}$ .
B. $\dfrac{4}{3}\pi {{r}^{3}}$
C. $4\pi {{r}^{2}}$
D. $\dfrac{4}{3}\pi {{r}^{2}}$

Answer 1

Hint: Volume of the sphere is $\dfrac{2}{3}rd$ of the volume of the cylinder. The diagram of the sphere is equal to the height of the cylinder. Draw a figure of a sphere inscribed in a cylinder to get the volume of sphere

Complete step-by-step answer:
The volume of the sphere is the capacity it has. We can know that the shape of the sphere is round and three – dimensional. It has three axis such as x,y and z axis, which defines its shape. For example football and basketball represent spheres which have volume.
The volumes of a sphere depend upon the diameter of radius and the sphere. Now if we take the cross – section of sphere of sphere it is a circle when the circle is rotated, we can observe the change in shape.

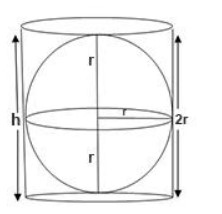
To find the formula of the sphere, we can be the Archimedes principle.
Archimedes’ principle helps us find the volume of a spherical object. It states that when a solid object is engaged in a container filled with water, the volume of the solid object can be obtained. Because the volume of water that flows from the container is equal to the volume of the spherical object.
Let the volume of the spherical object be $\dfrac{2}{3}rd$ of the cylindrical container.
$\therefore \text{volume of sphere =}\dfrac{2}{3}rd\text{ of volume of cylinder}\text{.}$
We know that the volume of cylinder $=\pi {{r}^{2}}h.$
Where r and h is the radius and height of the cylinder. From the figure. We can say that, $h=2r$ . where 2r is the diameter of the sphere. Thus the diameter of the sphere is equal to the height of the cylinder. We have been given that radius, $r=\pi cm$ .
Now, $\text{volume of sphere =}\dfrac{2}{3}rd\text{ of volume of cylinder}\text{.}$
$\therefore \text{ Volume of sphere =}\dfrac{2}{3}\times \pi {{r}^{2}}h$ .
$\because h=2r\text{ and put r}=\pi .$
Thus volume of sphere $=\dfrac{2}{3}\pi {{r}^{2}}\left( 2r \right)=\dfrac{4}{3}\pi {{r}^{3}}=\dfrac{4}{3}\pi {{\left( \pi \right)}^{3}}=\dfrac{4}{3}{{\pi }^{4}}$ .
Hence we get the volume of the sphere as $\dfrac{4}{3}{{\pi }^{4}}$ .
$\therefore $ option (A) is the correct answer.

Note: Volume of sphere is a basic formula, which you should know without deriving it. We have been given radius of sphere as $\pi cm$ don’t forget to substitute $r=\pi cm$ or else you will get the final answer as $\dfrac{4}{3}\pi {{r}^{3}}$ . Which is option (B) and the wrong answer.