Question

The volume of a right circular cone is $320\pi {\text{ c}}{{\text{m}}^3}$ and the radius of its base is 8cm. Find the slant height, curved surface area and the total surface area. Give your answers in terms of $\pi $.

Answer 1

Hint: In this question use the direct formula for the volume of the right circular cone which is $\dfrac{1}{3}\pi {r^2}h$ to take out the height of the cone. Slant height could easily be calculated by using Pythagoras theorem as the radius, slant height and height of cone forms a right angle triangle (see figure). For total surface area and curved surface area use the direct formula.

Complete step-by-step answer:

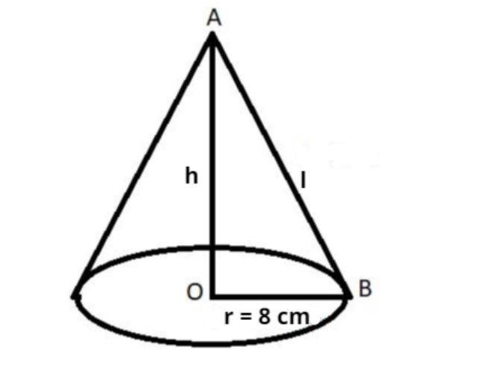
The pictorial representation of the right circular cone is shown above.
Now the volume of the right circular cone is $320\pi $$cm^3$ (given).
And the base radius of the cone is 8 cm (given).
Let h and l be the height and slant height of the cone as shown in figure.
Now as we know that the volume (V) of the cone is $\dfrac{1}{3}\pi {r^2}h$.
$ \Rightarrow V = \dfrac{1}{3}\pi {r^2}h$ $cm^3$
Now substitute all the values in the above equation we have,
\[ \Rightarrow 320\pi = \dfrac{1}{3}\pi {.8^2}h\]
Now simplify it and calculate the height of the cone we have,
\[ \Rightarrow h = \dfrac{{320 \times 3}}{{8 \times 8}} = 15\] cm
So in triangle AOB apply Pythagoras Theorem we have,
\[ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}\]
$ \Rightarrow {l^2} = {h^2} + {r^2}$
$ \Rightarrow {l^2} = {15^2} + {8^2} = 225 + 64 = 289 = {\left( {17} \right)^2}$
$ \Rightarrow l = 17$ cm
So the slant height of the cone is 17 cm.
Now as we know that the curved surface area (C.S.A) of the cone is $\left( {\pi rl} \right)$ sq. cm.
 $ \Rightarrow C.S.A = \pi \left( 8 \right)\left( {17} \right) = 136\pi {\text{ c}}{{\text{m}}^2}$
And we also know that the total surface area (T.S.A) of the cone is the sum of C.S.A and the area of the circular base.
$ \Rightarrow T.S.A = C.S.A + \pi {r^2}$ where $\pi {r^2}$ is the area of circular base having radius r.
$ \Rightarrow T.S.A = 136\pi + \pi {\left( 8 \right)^2} = 136\pi + 64\pi = 200\pi {\text{ c}}{{\text{m}}^2}$
So the slant height, curved surface area and the total surface area of the cone is 17 cm, $136\pi {\text{ c}}{{\text{m}}^2}$ and $200\pi {\text{ c}}{{\text{m}}^2}$ respectively.
So this is the required answer.

Note: There is always a confusion regarding total surface area and curved surface area. The curved surface area is for the curved surfaces only and it excludes the base area of the right circular cone which is eventually a circle, however the total surface area includes all curved surfaces along with the base area that’s why it’s formula is curved surface area + the area of circular base which is $\pi {r^2}$. This basic understanding will help not to make any mistake in such C.S.A and T.S.A based questions.