Question

The volume of a material of a hollow sphere with external radius \[10{\text{ cm}}\] and internal diameter \[{\text{6 cm}}\] is nearly
A. \[4077{\text{ c}}{{\text{m}}^3}\]
B. \[4070{\text{ c}}{{\text{m}}^3}\]
C. \[4007{\text{ c}}{{\text{m}}^3}\]
D. \[4073{\text{ c}}{{\text{m}}^3}\]

Answer 1

Hint:In the question we are asked to find the volume of the material enclosed between two spheres. For this we will first find the volumes of the two spheres by using the formula and then we will subtract the smaller volume from the bigger volume to get the volume of the material enclosed between the two spheres.

Formula used:
Volume of sphere \[ = \dfrac{4}{3}\pi {r^3}\]
\[r = \] radius of the sphere.

Complete step by step answer:

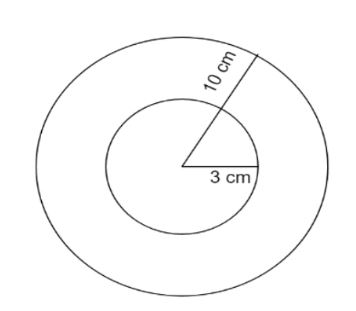
Let the radius of inner sphere be \[ = r{\text{ cm}}\]
Radius of outer sphere \[ = R{\text{ cm}}\]
From the question we have the internal diameter \[ = 6{\text{ cm}}\]
So, the internal radius, \[r = 3{\text{ cm}}\].
Also, we have \[R = 10{\text{ cm}}\]
We know that;
Volume of sphere \[ = \dfrac{4}{3}\pi {r^3}\]
So, the volume of outer sphere \[ = \dfrac{4}{3}\pi {R^3}{\text{ c}}{{\text{m}}^3}\]

Putting the value of outer radius, we get;
\[\text{Volume of outer sphere} = \dfrac{4}{3}\pi {\left( {10} \right)^3}{\text{ c}}{{\text{m}}^3}\]
On calculation we get;
\[ \text{Volume of outer sphere}= 4190.476{\text{ c}}{{\text{m}}^3}\]
Similarly, the volume of the inner sphere \[ = \dfrac{4}{3}\pi {r^3}\]
Putting the value of inner radius, we get;
\[\text{Volume of outer sphere} = \dfrac{4}{3}\pi {\left( 3 \right)^3}{\text{ c}}{{\text{m}}^3}\]
\[\Rightarrow \text{Volume of outer sphere}= 113.142{\text{ c}}{{\text{m}}^3}\]

Now to find the volume of the enclosed material we will subtract the volume of the inner sphere from the volume of the outer sphere.
So,
The volume of enclosed material \[ = \] volume of outer sphere \[ - \] volume of inner sphere
\[\text{Volume of enclosed material} = 4190.476{\text{ c}}{{\text{m}}^3} - 113.142{\text{ c}}{{\text{m}}^3}\]
\[\therefore \text{Volume of enclosed material} = 4077.334{\text{ c}}{{\text{m}}^3}\]
Which is nearly equal to \[4077{\text{ c}}{{\text{m}}^3}\].

Hence, the correct answer is option A.

Note:One major mistake that students commit is that they simply put the given values in the formula for finding the volume but, we cannot do that because here the given data are different. In the question it is given about the internal diameter and not the internal radius. So, first we need to calculate the internal radius and then use that in the formula.Also, we have to keep in mind whether the given units are the same or not.