Question

The volume of a cube with diagonal of length d units is $\dfrac{{{d}^{3}}}{3\sqrt{3}}$ cu.units.
State True or False.
A. True
B. False
C. Data insufficient
D. None of the above

Answer 1

Hint: The diagonal of a cube is one that cuts through the centre of the cube. The diagonal on the face of the cube is not the diagonal. Find the relation between the diagonal & side of the cube then find the volume of the cube by substituting the side of the cube w.r.t to the diagonal.

Complete step by step answer:

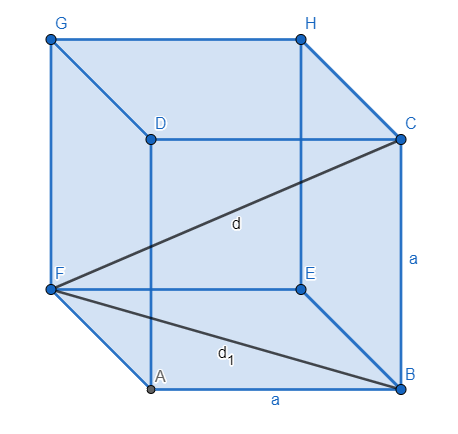
We know that a cube is a three dimensional solid. Now ‘a’ in a cube all the lengths are same. We can say that the length, width and height are equal and each of its faces is a square. The main diagonal of a cube is the one that cuts through the centre of the cube, the diagonal of a face of a cube is not the main diagonal.
Now let ‘a’ be the side of the cube and it is given that the length of the diagonal of the cube is ‘d’ units. In the figure you can see the diagonal ‘d’ and side ‘a’ of the cube.
To find the length of the diagonal, first let us consider the face ABEF. Its diagonal in the diagram is ${{d}_{1}}$.
Now, if we consider triangle ABF, it is a right-angled triangle with length of two sides as a and length of hypotenuse as ${{d}_{1}}$.
According to Pythagoras theorem, length of square of the hypotenuse is equal to the sum of the squares of the length of the sides.
$\begin{align}
  & \therefore {{\left( {{d}_{1}} \right)}^{2}}={{a}^{2}}+{{a}^{2}} \\
 & \therefore {{d}_{1}}=\sqrt{2}a \\
\end{align}$
Now consider triangle BCF, which is a right-angled triangle with length of one side a, length of the other side as $\sqrt{2}a$ and length of the hypotenuse as d.
Applying Pythagoras theorem, we get
$\begin{align}
  & {{d}^{2}}=2{{a}^{2}}+{{a}^{2}} \\
 & {{d}^{2}}=3{{a}^{2}} \\
 & d=\sqrt{3}a \\
\end{align}$
$\therefore $ Length of diagonal of cube of side a is $d=a\sqrt{3}$ .
$\therefore a=\dfrac{d}{\sqrt{3}}$ .
We know the formula for finding the volume of a cube. Put $a=\dfrac{d}{\sqrt{3}}$
$\therefore $ volume of cube $={{a}^{3}}={{\left( \dfrac{d}{\sqrt{3}} \right)}^{3}}=\dfrac{{{d}^{3}}}{3\sqrt{3}}$ .
We have been told that the volume of the cube is $\dfrac{{{d}^{3}}}{3\sqrt{3}}$ cu.units, which is same as the answer we got.
$\therefore $The volume of a cube with diagonal of length d units $=\dfrac{{{d}^{3}}}{3\sqrt{3}}$ cu.units.
$\therefore $The statement is true.

So, the correct answer is “Option A”.

Note: Cube is one of the easiest portions that you can learn in shape. The properties of cube are easier to remember than cuboids etc. in this problem, it was the direct application of the components that were given to us. Just by reading the question, most students mark option C as the correct answer because they think that only diagonal is given and it is not possible to find the volume. They must not jump into such conclusions, instead go through the concerts, relate the side length and diagonal and perform the calculations to arrive at the correct answer.