Question

The vertices of the triangle are \[\left( {6,0} \right)\] , \[\left( {0,6} \right)\] and \[\left( {6,6} \right)\] . The distance between its circumcenter and centroid is
A.\[2\]
B.\[\sqrt 2 \]
C.\[1\]
D\[2\sqrt 2 \]

Answer 1

Hint: In the question related to the vertices of a triangle , always draw a figure for better understanding . The two of its vertices will act as the coordinates of the diameter of the circumcircle inscribed . For finding the centroid we have the formula for it .

Complete step-by-step answer:
Given : \[\left( {6,0} \right)\] , \[\left( {0,6} \right)\] and \[\left( {6,6} \right)\] . We draw the triangle using these vertices

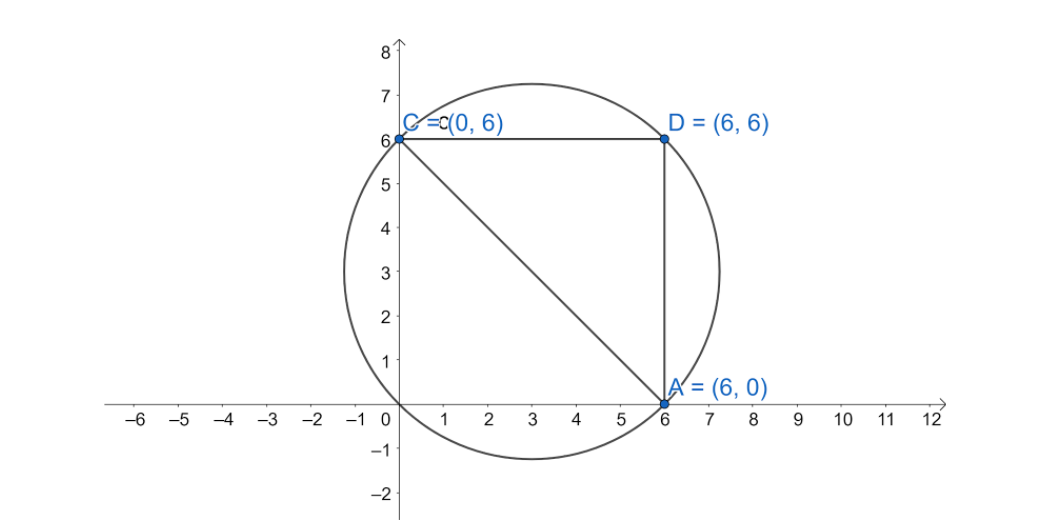
From the figure we get that the coordinates \[\left( {6,0} \right)\] and \[\left( {0,6} \right)\] will act as the diameter of the circle .
Therefore , the circumcenter of the circle will be \[ = \left( {\dfrac{{0 + 6}}{2},\dfrac{{6 + 0}}{2}} \right)\] , on solving we get
 \[ = \left( {3,3} \right)\] .
You can also understand that we are finding the midpoint of the diameter which will be the circumcenter .
Now , for the centroid we use the formula \[ = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)\] , on putting the values we get ,
\[ = \left( {\dfrac{{0 + 6 + 6}}{3},\dfrac{{6 + 0 + 6}}{3}} \right)\] , on solving we get ,
\[ = \left( {4,4} \right)\] .
This is the coordinates for centroid .
Now , for the distance between circumcenter and centroid we will use distance formula \[ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \] .
On putting the values we get ,
\[ = \sqrt {{{\left( {4 - 3} \right)}^2} + {{\left( {4 - 3} \right)}^2}} \]
\[ = \sqrt {{1^2} + {1^2}} \] , on solving we get
\[ = \sqrt 2 \]
Therefore , option (B) is the correct answer .
So, the correct answer is “Option B”.

Note: The centroid of a triangle is the intersection of the three medians of the triangle ( each median connecting a vertex with the midpoint of the opposite side ) . The circumcenter is the center point of the circumcircle drawn around a polygon. This means that the perpendicular bisectors of the triangle are concurrent (i.e. meeting at one point) .