Question

The vertices of the triangle are A(5,4,6), B(1,−1,3) and C(4,3,2). The internal bisector of angle A meets BC at D, then the length of AD is:
\[
  A.\dfrac{1}{8}\sqrt {170} \\
  B.\dfrac{3}{8}\sqrt {170} \\
  C.\dfrac{5}{8}\sqrt {170} \\
  D.\dfrac{7}{8}\sqrt {170} \\
 \]

Answer 1

Hint: This is the case of three dimensional coordinate geometry. First we will find the length of the sides AB and AC. Then find the coordinate of point D by using section formula. Using the distance formula length of AD can be easily computed.

Complete step-by-step answer:
     

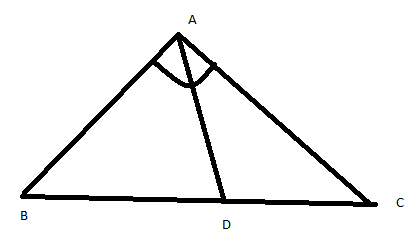
In triangle ABC, the internal bisector of angle A will meet BC at D. As from the geometry, we know that any angle bisector in the triangle will bisect the opposite side in the ratio of the other two sides.
Thus, according to angle bisector theorem, we have
$\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{CD}}$…(1)
Distance formula for points\[({x_1},{y_1},{z_1}) and ({x_2},{y_2},{z_2})\] is:
\[\sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2} + {{({z_1} - {z_2})}^2}} \]
Since coordinates of A , B and C are (5,4,6), (1,−1,3) and (4,3,2). We will calculate lengths of AB and AC by using distance formula as follows.
$
  AB = \sqrt {{{(1 - 5)}^2} + {{( - 1 - 4)}^2} + {{(3 - 6)}^2}} \\
   = \sqrt {16 + 25 + 9} \\
   = 5\sqrt 2 \\
 $
$
  AC = \sqrt {{{(4 - 5)}^2} + {{(3 - 4)}^2} + {{(2 - 6)}^2}} \\
   = \sqrt {1 + 1 + 16} \\
   = 3\sqrt 2 \\
 $
Thus from equation (1) , we get
$
  \dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{CD}} = \dfrac{{5\sqrt 2 }}{{3\sqrt 2 }} \\
   \Rightarrow \dfrac{{BD}}{{CD}} = \dfrac{5}{3} \\
 $….(2)
Now, point D will divide the BC in a ratio of 5:3.
So, by section formula,
$
  x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}} \\
  y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}} \\
  z = \dfrac{{m{z_2} + n{z_1}}}{{m + n}} \\
 $
Putting coordinates of B and C with m=5 and n=3 in above formula, we get
$
  x = \dfrac{{5 \times 4 + 3 \times 1}}{{5 + 3}} = \dfrac{{23}}{8} \\
  y = \dfrac{{5 \times 3 - 3 \times 1}}{{5 + 3}} = \dfrac{{12}}{8} \\
  z = \dfrac{{5 \times 2 + 3 \times 3}}{{5 + 3}} = \dfrac{{19}}{8} \\
 $
So coordinate of D is $(\dfrac{{23}}{8},\dfrac{{12}}{8},\dfrac{{19}}{8})$. Now, we will find the distance between A and D, to get length of AD by using distance formula as follows,
\[
  AD = \sqrt {{{(5 - \dfrac{{23}}{8})}^2} + {{(4 - \dfrac{{12}}{8})}^2} + {{(6 - \dfrac{{19}}{8})}^2}} \\
   = \sqrt {{{(\dfrac{{17}}{8})}^2} + {{(\dfrac{{20}}{8})}^2} + {{(\dfrac{{29}}{8})}^2}} \\
   = \dfrac{1}{8}\sqrt {1530} \\
   = \dfrac{3}{8}\sqrt {170} \\
 \]
Thus the length of AD will be $\dfrac{3}{8}\sqrt {170} $.

So, the correct answer is “Option B”.

Note: Proper use of formula in coordinate geometry is very important. Distance and section formulas are used in the above problem. Careful substitution of the values of coordinates and other terms is needed to get the correct result. Also, sometimes theorems from the geometry will be used appropriately to proceed in the solution.