
The vertices of a triangle are A \[[m,n]\], B \[[12,19]\] and C \[\left[ {23,20} \right]\]. Its area is 70 square units. If the slope of the median through A is \[ - 5\], then \[\left[ {m + n} \right]\] is.
A. 17
B. 48
C. 57
D. 32
Answer
585.9k+ views
Hint:
We will use the information that a median divides the line into two equal parts which will help in determining the coordinates of D. Furthermore, using the slope, coordinates of D and A, we will determine the line AD which will give the required relation. We will use the equation of area of the triangle to determine the second equation.
Formula Used: We will use the formulae:
1) \[\left[ {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right]\] where \[\left[ {{x_1},{y_1}} \right]\] and \[\left[ {{x_2},{y_2}} \right]\] are the coordinates of the endpoints and
2) \[y = ax + c\] where \[x\], \[y\], \[a\] and \[c\] are the \[x - \]coordinate, \[y - \]coordinate, slope, and \[y\]intercept.
3) The area of the triangle whose coordinates of all the three points are given, is determined by the formula \[\Delta = \dfrac{1}{2}\left[ {{x_1}\left[ {{y_2} - {y_3}} \right] + {x_2}\left[ {{y_3} - {y_1}} \right] + {x_3}\left[ {{y_1} - {y_2}} \right]} \right]\] where \[\left[ {{x_1},{y_1}} \right]\], \[\left[ {{x_2},{y_2}} \right]\], \[\left[ {{x_3},{y_3}} \right]\] are the coordinates of the B, C and A.
Complete step by step solution:
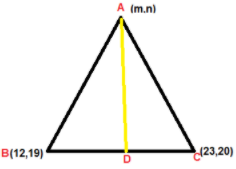
To determine the value of \[m\] and \[n\], we need to obtain two equations. The first equation will be obtained from using the median information and the second equation will be obtained using the area of the triangle.
A median is a line which divides the line it falls through, into two equal parts. This tells us that point D is the middle point of line BC. To calculate the middle point we will use the formula. \[\left[ {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right]\] where \[\left[ {{x_1},{y_1}} \right]\] and \[\left[ {{x_2},{y_2}} \right]\] are the coordinates of the endpoints.
Substituting \[\left[ {{x_1},{y_1}} \right] = \left[ {12,19} \right]\] and \[\left[ {{x_2},{y_2}} \right] = \left[ {23,20} \right]\], we get,
\[\left[ {\dfrac{{12 + 23}}{2},\dfrac{{19 + 20}}{2}} \right] = \left[ {\dfrac{{35}}{2},\dfrac{{39}}{2}} \right]\]
So the coordinates of D are \[\left[ {\dfrac{{35}}{2},\dfrac{{39}}{2}} \right]\].
As given that the slope of the line AD is \[ - 5\], we will use this information to form the equation of line AD.
In the equation of line \[y = ax + c\], substitute \[x = \dfrac{{35}}{2}\], \[y = \dfrac{{39}}{2}\] and \[a = - 5\] so as to obtain the value of \[c\].
\[\dfrac{{39}}{2} = \left[ { - 5} \right]\left[ {\dfrac{{35}}{2}} \right] + c\\ \Rightarrow \dfrac{{39}}{2} = \dfrac{{ - 175}}{2} + c\\ \Rightarrow \dfrac{{39}}{2} + \dfrac{{175}}{2} = c\]
Simplify the equations further.
\[\dfrac{{214}}{2} = c\\ \Rightarrow 107 = c\]
So the equation of line AD is \[y = - 5x + 107\]. Since the point A also lies on the line AD, the coordinates of A which are \[\left[ {m,n} \right]\] will satisfy the equation of line AD as well.
Substitute \[\left[ {x,y} \right] = \left[ {m,n} \right]\] into the equation, we get,
\[n = - 5m + 107\\ \Rightarrow 5m + n = 107...............\left[ i \right]\]
Secondly, the area of the triangle whose coordinates of all the three points are given, is determined by the formula \[\Delta = \dfrac{1}{2}\left[ {{x_1}\left[ {{y_2} - {y_3}} \right] + {x_2}\left[ {{y_3} - {y_1}} \right] + {x_3}\left[ {{y_1} - {y_2}} \right]} \right]\] where \[\left[ {{x_1},{y_1}} \right]\], \[\left[ {{x_2},{y_2}} \right]\], \[\left[ {{x_3},{y_3}} \right]\] are the coordinates of the B, C and A.
Substitute \[\Delta = 70\], \[\left[ {{x_1},{y_1}} \right] = \left[ {12,19} \right]\], \[\left[ {{x_2},{y_2}} \right] = \left[ {23,20} \right]\] and \[\left[ {{x_3},{y_3}} \right] = \left[ {m,n} \right]\] in the equation.
\[70 = \dfrac{1}{2}\left[ {12\left[ {20 - n} \right] + 23\left[ {n - 19} \right] + m\left[ {19 - 20} \right]} \right]\\70 = \dfrac{1}{2}\left[ {240 - 12n + 23n - 437 - m} \right]\]
Simplify further so as to obtain the relation between \[m\] and \[n\].
\[70 \times 2 = - 197 + 11n - m\\140 = - 197 + 11n - m\\11n - m = 197 + 140\\11n - m = 337................\left[ {ii} \right]\]
Now to solve the system of pair equations, we will use the method of substitution.
Let us consider the equation \[5m + n = 107\] in which we will substitute the value of \[n\] and the equation \[11n - m = 337\] from which we derive its value.
Subtract \[m\] from both the sides and then divide both the sides with 11, so as to obtain the value of \[n\].
\[11n = 337 + m\\ \Rightarrow n = \dfrac{{337 + m}}{{11}}\]
Now, replace this above obtained value of \[n\] in the equation \[5m + n = 107\] to obtain the value of \[m\].
Substitute \[n = \dfrac{{337 + m}}{{11}}\] in the equation.
\[5m + \dfrac{{337 + m}}{{11}} = 107\]
Now, as we can see that the second term has a denominator 11 but \[5m\] does not have the same. So as to introduce a denominator to \[5m\], we will need to multiply the denominator and the numerator with 11 as well.
\[\dfrac{{5m}}{1} \times \dfrac{{11}}{{11}} + \dfrac{{337 + m}}{{11}} = 107\\ \Rightarrow \dfrac{{55m + 337 + m}}{{11}} = 107\]
Once we achieve denominators, we can add the numerators.
\[55m + 337 + m = 107 \times 11\\ \Rightarrow 56m + 337 = 1177\\ \Rightarrow 56m = 1177 - 337\]
Simplify the equation further to obtain the value of \[m\].
\[56m = 840\\m = \dfrac{{840}}{{56}}\\m = 15\]
We will substitute \[m = 15\] in the equation \[n = \dfrac{{337 + m}}{{11}}\] in order to obtain the value of \[n\].
\[n = \dfrac{{337 + 15}}{{11}}\\ = \dfrac{{352}}{{11}}\\ = 32\]
We need to determine the sum of the \[m\] and \[n\]. Substitute \[m = 15\] and \[n = 32\] in the expression \[m + n\].
\[m + n = 15 + 32\\ = 47\]
So, 47 is the value of \[m + n\].
Note:
Alternatively, the value of \[m\] and \[n\] can be derived even if we deduce the value of \[m\] from the equation.
\[m = 11n - 337\]
Now, we will substitute this above obtained value of \[m\] in the equation \[5m + n = 107\] to obtain the value of \[n\].
Substituting \[m = 11n - 337\] in the equation, we get
\[5\left[ {11n - 337} \right] + n = 107\\ \Rightarrow 55n - 1685 + n = 107\\ \Rightarrow 56n = 107 + 1685\]
Simplify the equation further to obtain the value of \[n\].
\[56n = 1792\\n = \dfrac{{1792}}{{56}}\\n = 32\]
We will substitute \[n = 32\]in the equation \[m = 11n - 337\] in order to obtain the value of \[m\].
\[m = 11\left[ {32} \right] - 337\\ = 352 - 337\\ = 15\]
Then,
\[m + n = 32 + 15\\ = 47\]
So, 47 is the value of \[m + n\].
We will use the information that a median divides the line into two equal parts which will help in determining the coordinates of D. Furthermore, using the slope, coordinates of D and A, we will determine the line AD which will give the required relation. We will use the equation of area of the triangle to determine the second equation.
Formula Used: We will use the formulae:
1) \[\left[ {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right]\] where \[\left[ {{x_1},{y_1}} \right]\] and \[\left[ {{x_2},{y_2}} \right]\] are the coordinates of the endpoints and
2) \[y = ax + c\] where \[x\], \[y\], \[a\] and \[c\] are the \[x - \]coordinate, \[y - \]coordinate, slope, and \[y\]intercept.
3) The area of the triangle whose coordinates of all the three points are given, is determined by the formula \[\Delta = \dfrac{1}{2}\left[ {{x_1}\left[ {{y_2} - {y_3}} \right] + {x_2}\left[ {{y_3} - {y_1}} \right] + {x_3}\left[ {{y_1} - {y_2}} \right]} \right]\] where \[\left[ {{x_1},{y_1}} \right]\], \[\left[ {{x_2},{y_2}} \right]\], \[\left[ {{x_3},{y_3}} \right]\] are the coordinates of the B, C and A.
Complete step by step solution:

To determine the value of \[m\] and \[n\], we need to obtain two equations. The first equation will be obtained from using the median information and the second equation will be obtained using the area of the triangle.
A median is a line which divides the line it falls through, into two equal parts. This tells us that point D is the middle point of line BC. To calculate the middle point we will use the formula. \[\left[ {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right]\] where \[\left[ {{x_1},{y_1}} \right]\] and \[\left[ {{x_2},{y_2}} \right]\] are the coordinates of the endpoints.
Substituting \[\left[ {{x_1},{y_1}} \right] = \left[ {12,19} \right]\] and \[\left[ {{x_2},{y_2}} \right] = \left[ {23,20} \right]\], we get,
\[\left[ {\dfrac{{12 + 23}}{2},\dfrac{{19 + 20}}{2}} \right] = \left[ {\dfrac{{35}}{2},\dfrac{{39}}{2}} \right]\]
So the coordinates of D are \[\left[ {\dfrac{{35}}{2},\dfrac{{39}}{2}} \right]\].
As given that the slope of the line AD is \[ - 5\], we will use this information to form the equation of line AD.
In the equation of line \[y = ax + c\], substitute \[x = \dfrac{{35}}{2}\], \[y = \dfrac{{39}}{2}\] and \[a = - 5\] so as to obtain the value of \[c\].
\[\dfrac{{39}}{2} = \left[ { - 5} \right]\left[ {\dfrac{{35}}{2}} \right] + c\\ \Rightarrow \dfrac{{39}}{2} = \dfrac{{ - 175}}{2} + c\\ \Rightarrow \dfrac{{39}}{2} + \dfrac{{175}}{2} = c\]
Simplify the equations further.
\[\dfrac{{214}}{2} = c\\ \Rightarrow 107 = c\]
So the equation of line AD is \[y = - 5x + 107\]. Since the point A also lies on the line AD, the coordinates of A which are \[\left[ {m,n} \right]\] will satisfy the equation of line AD as well.
Substitute \[\left[ {x,y} \right] = \left[ {m,n} \right]\] into the equation, we get,
\[n = - 5m + 107\\ \Rightarrow 5m + n = 107...............\left[ i \right]\]
Secondly, the area of the triangle whose coordinates of all the three points are given, is determined by the formula \[\Delta = \dfrac{1}{2}\left[ {{x_1}\left[ {{y_2} - {y_3}} \right] + {x_2}\left[ {{y_3} - {y_1}} \right] + {x_3}\left[ {{y_1} - {y_2}} \right]} \right]\] where \[\left[ {{x_1},{y_1}} \right]\], \[\left[ {{x_2},{y_2}} \right]\], \[\left[ {{x_3},{y_3}} \right]\] are the coordinates of the B, C and A.
Substitute \[\Delta = 70\], \[\left[ {{x_1},{y_1}} \right] = \left[ {12,19} \right]\], \[\left[ {{x_2},{y_2}} \right] = \left[ {23,20} \right]\] and \[\left[ {{x_3},{y_3}} \right] = \left[ {m,n} \right]\] in the equation.
\[70 = \dfrac{1}{2}\left[ {12\left[ {20 - n} \right] + 23\left[ {n - 19} \right] + m\left[ {19 - 20} \right]} \right]\\70 = \dfrac{1}{2}\left[ {240 - 12n + 23n - 437 - m} \right]\]
Simplify further so as to obtain the relation between \[m\] and \[n\].
\[70 \times 2 = - 197 + 11n - m\\140 = - 197 + 11n - m\\11n - m = 197 + 140\\11n - m = 337................\left[ {ii} \right]\]
Now to solve the system of pair equations, we will use the method of substitution.
Let us consider the equation \[5m + n = 107\] in which we will substitute the value of \[n\] and the equation \[11n - m = 337\] from which we derive its value.
Subtract \[m\] from both the sides and then divide both the sides with 11, so as to obtain the value of \[n\].
\[11n = 337 + m\\ \Rightarrow n = \dfrac{{337 + m}}{{11}}\]
Now, replace this above obtained value of \[n\] in the equation \[5m + n = 107\] to obtain the value of \[m\].
Substitute \[n = \dfrac{{337 + m}}{{11}}\] in the equation.
\[5m + \dfrac{{337 + m}}{{11}} = 107\]
Now, as we can see that the second term has a denominator 11 but \[5m\] does not have the same. So as to introduce a denominator to \[5m\], we will need to multiply the denominator and the numerator with 11 as well.
\[\dfrac{{5m}}{1} \times \dfrac{{11}}{{11}} + \dfrac{{337 + m}}{{11}} = 107\\ \Rightarrow \dfrac{{55m + 337 + m}}{{11}} = 107\]
Once we achieve denominators, we can add the numerators.
\[55m + 337 + m = 107 \times 11\\ \Rightarrow 56m + 337 = 1177\\ \Rightarrow 56m = 1177 - 337\]
Simplify the equation further to obtain the value of \[m\].
\[56m = 840\\m = \dfrac{{840}}{{56}}\\m = 15\]
We will substitute \[m = 15\] in the equation \[n = \dfrac{{337 + m}}{{11}}\] in order to obtain the value of \[n\].
\[n = \dfrac{{337 + 15}}{{11}}\\ = \dfrac{{352}}{{11}}\\ = 32\]
We need to determine the sum of the \[m\] and \[n\]. Substitute \[m = 15\] and \[n = 32\] in the expression \[m + n\].
\[m + n = 15 + 32\\ = 47\]
So, 47 is the value of \[m + n\].
Note:
Alternatively, the value of \[m\] and \[n\] can be derived even if we deduce the value of \[m\] from the equation.
\[m = 11n - 337\]
Now, we will substitute this above obtained value of \[m\] in the equation \[5m + n = 107\] to obtain the value of \[n\].
Substituting \[m = 11n - 337\] in the equation, we get
\[5\left[ {11n - 337} \right] + n = 107\\ \Rightarrow 55n - 1685 + n = 107\\ \Rightarrow 56n = 107 + 1685\]
Simplify the equation further to obtain the value of \[n\].
\[56n = 1792\\n = \dfrac{{1792}}{{56}}\\n = 32\]
We will substitute \[n = 32\]in the equation \[m = 11n - 337\] in order to obtain the value of \[m\].
\[m = 11\left[ {32} \right] - 337\\ = 352 - 337\\ = 15\]
Then,
\[m + n = 32 + 15\\ = 47\]
So, 47 is the value of \[m + n\].
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




