Question

The vertices of a triangle are A (m, n), B (12, 19) and C (23, 20). Its area is 70 square units. If the slope of the median through A is -5, then\[\left( {m + n} \right)\]is.
A) 17
B) 48
C) 57
D) 32
E) 47

Answer 1

Hint: Here we will first find the coordinates of D which is the midpoint of BC. Then we will find the slope of AD and equate it equal to the given value and then we will finally use the given value of area and solve for the values of m and n and then find the desired value.
The midpoint (x, y) of two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\]is given by:-
\[x = \dfrac{{{x_1} + {x_2}}}{2};y = \dfrac{{{y_1} + {y_2}}}{2}\]
The area of triangle with vertices \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)\] is given by:-
\[area = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]\].
The slope of a line with endpoints \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is given by:-
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]

Complete step-by-step answer:

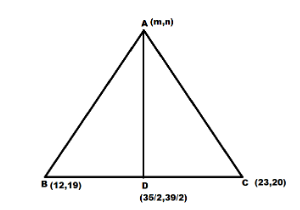
First here we will find the coordinates of point D which is the midpoint of BC.
Now we know that, the midpoint (x, y) of two points \[\left( {{x_1},{y_1}} \right)\]and \[\left( {{x_2},{y_2}} \right)\] is given by:-
\[x = \dfrac{{{x_1} + {x_2}}}{2};y = \dfrac{{{y_1} + {y_2}}}{2}\]
Hence, the point D is given by:-
\[x = \dfrac{{12 + 23}}{2};y = \dfrac{{19 + 20}}{2}\]
Simplifying it further we get:-
$\Rightarrow$\[x = \dfrac{{35}}{2};y = \dfrac{{39}}{2}\]
Therefore, the coordinates of D are \[D\left( {\dfrac{{35}}{2},\dfrac{{39}}{2}} \right)\].
Now it is given that the slope of AD is -5.
We know that, slope of a line with endpoints \[\left( {{x_1},{y_1}} \right)\]and \[\left( {{x_2},{y_2}} \right)\] is given by:-
$\Rightarrow$\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]
Hence, the slope of AD is given by:-
\[{m_{AD}} = \dfrac{{n - \dfrac{{39}}{2}}}{{m - \dfrac{{35}}{2}}}\]
Putting the value of slope we get:-
$\Rightarrow$\[ - 5 = \dfrac{{n - \dfrac{{39}}{2}}}{{m - \dfrac{{35}}{2}}}\]
Simplifying it further we get:-
$\Rightarrow$\[ - 5 = \dfrac{{2n - 39}}{{2m - 35}}\]
Solving it further we get:-
$\Rightarrow$\[2n - 39 = - 10m + 175\]
\[ \Rightarrow 2n + 10m = 214\]
Dividing whole equation by 2 we get:-
\[5m + n = 107\]…………………….. (1)
Now we know that the area of triangle with vertices \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)\] is given by:-
\[area = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]\].
Hence, the area of triangle ABC is given by:-
$\Rightarrow$\[area = \dfrac{1}{2}\left[ {m\left( {19 - 20} \right) + 12\left( {20 - n} \right) + 23\left( {n - 19} \right)} \right]\]
Putting the given value of area we get:-
$\Rightarrow$\[70 = \dfrac{1}{2}\left[ {m\left( {19 - 20} \right) + 12\left( {20 - n} \right) + 23\left( {n - 19} \right)} \right]\]
Simplifying it further we get:-
$\Rightarrow$\[140 = - m + 240 - 12n + 23n - 437\]
\[ \Rightarrow - m + 11n = 337\]……………………….. (2)
Now solving equations 1 and 2 we get:-
Multiplying equation 2 by 5 we get:-
 \[ - 5m + 55n = 1685\]……………………….. (3)
Adding equation 1 and 3 we get:-
$\Rightarrow$\[56n = 107 + 1685\]
$\Rightarrow$\[56n = 1792\]
Evaluating for the value of n we get:-
\[n = 32\]
Putting this value in equation 1 we get:-
$\Rightarrow$\[5m + 32 = 107\]
Evaluating for the value of m we get:-
$\Rightarrow$\[5m = 75\]
\[ \Rightarrow m = 15\]
Hence, the value of \[\left( {m + n} \right)\] is given by:-
\[ \Rightarrow m + n = 32 + 15\]
\[ \Rightarrow m + n = 47\]

Hence option E is correct.

Note: Also, students might forget to add the values of m and n at last which can lead to wrong answers.
Slope of a line is defined as the ratio of change in y coordinate to the change in x coordinate.
\[slope = \dfrac{{{\text{change in y coordinate}}}}{{{\text{change in x coordinate}}}}\]
The area of the triangle with vertices \[\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)\]is also given in determinant form by:-
\[area = \dfrac{1}{2}\left[ {\begin{array}{*{20}{c}}
  {{x_1}}&{{x_2}}&{{x_3}} \\
  {{y_1}}&{{y_2}}&{{y_3}} \\
  {{z_1}}&{{z_2}}&{{z_3}}
\end{array}} \right]\]