Question

The vertices of a triangle are \[A( - 1, - 7),B(5,1)\] and \[C(1,4)\]. The equation of the bisector of \[\angle ABC\] is?
A. \[x - 7y + 2 = 0\]
B. \[x + y - 6 = 0\]
C. \[x + 2y - 7 = 0\]
D. \[116x - 39y = 157\]

Answer 1

Hint: To find the angle bisectors of the\[\angle ABC\], find equations of sides AB and BC and then use the formula of the bisector using those equations of AB and BC.

Complete step-by-step answer:
The vertices of the triangle are \[A( - 1, - 7),B(5,1)\] and \[C(1,4)\].

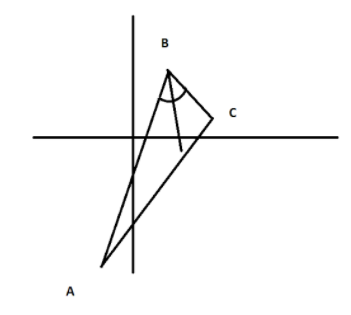
In two point form equation of a line joining two points (a,b) and (c,d),
\[y - d = \dfrac{{d - b}}{{c - a}}(x - c)\]
So if we find the equation of AB in two point form, we get,
\[y - 1 = \dfrac{{1 - ( - 7)}}{{5 - ( - 1)}}(x - 5)\]
On simplifying we get,
\[ \Rightarrow y - 1 = \dfrac{8}{6}(x - 5)\]
\[ \Rightarrow y - 1 = \dfrac{4}{3}(x - 5)\]
Multiplying with 3 we get,
\[ \Rightarrow 3y - 3 = 4x - 20\]
\[ \Rightarrow 3y - 4x + 17 = 0\]
Now, again in two point form, equation of BC,
\[
  y - 4 = \dfrac{{4 - 1}}{{1 - 5}}(x - 1) \\
   \Rightarrow y - 4 = - \dfrac{3}{4}(x - 1) \\
   \Rightarrow 4y - 16 = - 3x + 3 \\
   \Rightarrow 4y + 3x - 19 = 0 \\
  \]
Now, the equation of bisectors will be, \[{a_1}x + {b_1}y + {c_1} = 0\]and \[{a_2}x + {b_2}y + {c_2} = 0\]are given by, \[\left| {\dfrac{{{a_1}x + {b_1}y + {c_1}}}{{\sqrt {a_1^2 + b_1^2} }}} \right| = \pm \left| {\dfrac{{{a_2}x + {b_2}y + {c_2}}}{{\sqrt {a_2^2 + b_2^2} }}} \right|\]
So, The equation of the bisectors will be,
\[\left| {\dfrac{{3y - 4x + 17}}{{\sqrt {{3^2} + {4^2}} }}} \right| = \left| {\dfrac{{4y + 3x - 19}}{{\sqrt {{4^2} + {3^2}} }}} \right|\]
\[ \Rightarrow 3y - 4x + 17 = \pm (4y + 3x - 19)\]
So the bisectors will be,
\[3y - 4x + 17 = 4y + 3x - 19\]
\[ \Rightarrow 7x + y = 36\]
And
\[
  3y - 4x + 17 = - 4y - 3x + 19 \\
   \Rightarrow - x + 7y = 2 \\
  \]
So, equation of the bisectors of \[\angle ABC\] are \[7x + y = 36\] and \[ - x + 7y = 2\].
Hence, option (A) is correct.

Note: Every angle of a triangle has two bisectors one internal and one external. And here we found two equations one of them is internal and other is external, hence we should consider both the cases.