Question

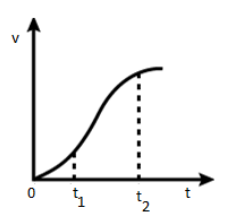
The velocity-time graph of a particle in one-dimensional motion is shown in Fig.
Which of the following formulas are correct for describing the motion of the particle over the time-interval $ {t_1} $ to $ {t_2} $ .
 $ \left( a \right)\;x\left( {{t_2}} \right) = x\left( {{t_{1}}} \right) + v\left( {{t_1}} \right)\left( {{t_2} - {t_1}} \right) + \left( {\dfrac{1}{2}} \right)a{\left( {{t_2} - {t_1}} \right)^2} \\
  \left( b \right)v\left( {{t_2}} \right) = v\left( {{t_1}} \right) + a\left( {{t_2} - {t_1}} \right) \\
  \left( c \right){v_{average}} = \dfrac{{\left( {x\left( {{t_2}} \right) - x\left( {{t_1}} \right)} \right)}}{{{t_2} - {t_1}}} \\
  \left( d \right){a_{average}} = \dfrac{{\left( {v\left( {{t_2}} \right) - v\left( {{t_1}} \right)} \right)}}{{{t_2} - {t_1}}} \\
  \left( e \right)x\left( {{t_2}} \right) = x\left( {{t_{1}}} \right) + {v_{average}}\left( {{t_2} - {t_1}} \right) + \left( {\dfrac{1}{2}} \right){a_{average}}{\left( {{t_2} - {t_1}} \right)^2} \\
  \left( f \right)x\left( {{t_2}} \right) - x\left( {{t_{1}}} \right) = area\,under\,the\,v - t\,curve\,bounded\,by\,the\,t - axis\,and\,the\,dotted\,line\,shown \\ $

Answer 1

Hint :In order to solve this question, we are going to first analyze the graph and the motion type of the particle, and based on the uniformity of the acceleration, we can tell which options are correct and which are not as which represent the correct equations for the motion of particle.
The slope of the curve is given by
 $ slope = \dfrac{{dv}}{{dt}} $
Acceleration of the particle is also given by this relation,
 $ a = \dfrac{{dv}}{{dt}} $

Complete Step By Step Answer:
In the given graph, as we can see that the velocity is first increasing in a linear manner but takes a slow turn after the time t.
Now, the rate of change of the velocity with respect to time is given by the slope of the curve.
i.e. $ slope = \dfrac{{dv}}{{dt}} $
Acceleration of the particle is also given by this relation,
 $ a = \dfrac{{dv}}{{dt}} $
Here, the slope of the curve is not constant.
Now, this is not a constant acceleration motion. And thus, Newton's equations of motion cannot be applied here.
Therefore, the correct formula for describing the motion of the particle are:
 $ \left( c \right){v_{average}} = \dfrac{{\left( {x\left( {{t_2}} \right) - x\left( {{t_1}} \right)} \right)}}{{{t_2} - {t_1}}} \\
  \left( d \right){a_{average}} = \dfrac{{\left( {v\left( {{t_2}} \right) - v\left( {{t_1}} \right)} \right)}}{{{t_2} - {t_1}}} \\
  \left( f \right)x\left( {{t_2}} \right) - x\left( {{t_{1}}} \right) = area\,under\,the\,v - t\,curve\,bounded\,by\,the\,t - axis\,and\,the\,dotted\,line\,shown \\ $
Now the other formulae that are in the three options,
 $ \left( a \right)\;x\left( {{t_2}} \right) = x\left( {{t_{1}}} \right) + v\left( {{t_1}} \right)\left( {{t_2} - {t_1}} \right) + \left( {\dfrac{1}{2}} \right)a{\left( {{t_2} - {t_1}} \right)^2} \\
  \left( b \right)v\left( {{t_2}} \right) = v\left( {{t_1}} \right) + a\left( {{t_2} - {t_1}} \right) \\
  \left( e \right)x\left( {{t_2}} \right) = x\left( {{t_{1}}} \right) + {v_{average}}\left( {{t_2} - {t_1}} \right) + \left( {\dfrac{1}{2}} \right){a_{average}}{\left( {{t_2} - {t_1}} \right)^2} \\ $
Cannot be described as the given graph has a non-uniform slope, that’s why these equations cannot describe the motion of the particle.
So, options, (c),(d), (f) are the correct answers.

Note :
Alternatively,
If we take the two points on the curve corresponding to the two time intervals $ {t_1} $ and $ {t_2} $ , and draw tangents on the two points such that the angles formed by the tangents with the horizontal axis are equal to $ \theta $ .

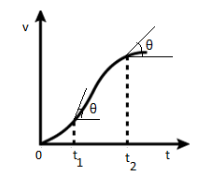
Here, $ slope = \tan \theta $