Question

The velocity of efflux is
(given ${{\rho }_{2}}=600kg\,{{m}^{3}}$, ${{\rho }_{1}}=900kg\,{{m}^{3}}$,$h=60cm$,$y=20cm$,(area of container)$A=0.5{{m}^{2}}$,(area of hole)$a=5c{{m}^{2}}$)
A.$10m{{s}^{-1}}$
B. $20m{{s}^{-1}}$
C. $4m{{s}^{-1}}$
D. $35m{{s}^{-1}}$

Answer 1

Hint: We will be using Bernoulli’s equation to find the velocity of efflux from the hole.Apply the Bernoulli equation at two points $A$ and $B$. Pressure at $A$ will be due to height $h$ and $\left( h-y \right)$ of the liquid whereas at B it will be atmospheric pressure. Also, we will use continuity equation to link velocity with the area of the container and the small hole.

Complete step by step answer:
The Bernoulli equation to be used is,
${{P}_{o}}+\rho gh+\dfrac{1}{2}\rho {{v}^{2}}$
So, following the procedure in the note, let velocity of efflux be ${{v}_{1}}$ ,and velocity inside the container as ${{v}_{2}}$and atmospheric pressure be ${{P}_{0}}$.
Pressure at A: ${{P}_{o}}+{{\rho }_{2}}gh+\left( h-y \right){{\rho }_{1}}g$
Pressure at A: ${{P}_{B}}$=${{P}_{0}}$
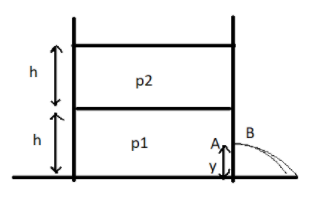
Consider two points $A$ (inside the cylinder) and $B$ (must outside the hole) in the same horizontal line as shown in the figure in question.
Apply Bernoulli equation at both these points,
${{P}_{o}}+hg{{\rho }_{2}}+\left( h-y \right){{\rho }_{1}}g+\dfrac{1}{2}{{\rho }_{2}}v_{2}^{2}+\left( hg{{\rho }_{2}}+\left( h-y \right){{\rho }_{1}}g \right)={{P}_{o}}+\dfrac{1}{2}{{\rho }_{1}}v_{1}^{2}+\left( hg{{\rho }_{2}}+\left( h-y \right){{\rho }_{1}}g \right)$
We will be using equation of continuity,
$A{{v}_{2}}=a{{v}_{1}}$
$\Rightarrow \dfrac{{{v}_{2}}}{{{v}_{1}}}=\dfrac{a}{A}$
Putting the values,
$\Rightarrow \dfrac{{{v}_{2}}}{{{v}_{1}}}=\dfrac{a}{A}=\dfrac{25\times {{10}^{-4}}}{0.5}$
$\Rightarrow \dfrac{{{v}_{2}}}{{{v}_{1}}}=\dfrac{25\times {{10}^{-4}}}{0.5}=50\times {{10}^{-4}}$
${{P}_{o}}+hg{{\rho }_{2}}+\left( h-y \right){{\rho }_{1}}g+\dfrac{1}{2}{{\rho }_{2}}v_{2}^{2}={{P}_{o}}+\dfrac{1}{2}{{\rho }_{1}}v_{1}^{2}$
Since the area of a hole is very small in comparison to base area A of the cylinder, velocity of liquid inside the cylinder is negligible.
So ${{v}_{2}}$ is negligible
Now the equation becomes,
$hg{{\rho }_{2}}+\left( h-y \right){{\rho }_{1}}g=\dfrac{1}{2}{{\rho }_{1}}v_{1}^{2}$
Substituting all the values,
$\Rightarrow 0.6\times 600\times 10+0.4\times 900\times 10=\dfrac{1}{2}\times 900\times v_{1}^{2}$
$\Rightarrow {{v}_{1}}=\sqrt{\dfrac{14400}{900}}$
$\Rightarrow {{v}_{1}}=4m{{s}^{-1}}$

So, the velocity of efflux has come out and according to it the correct option is C.

Note:
Bernoulli equation is applicable in case of incompressible, ideal and non-viscous fluid. It is used in case of fluid dynamics. There are many applications of Bernoulli equation like in spin of a ball, generating force during take-off of a plane and many more. Equation of continuity is also applicable in case of fluid dynamics.