
The vector $\overrightarrow {OA} $, where $O$ is the origin is given by $\overrightarrow {OA} = 2\widehat i + 2\widehat j$. Now it is rotated by $45^\circ $ anticlockwise about $O$. What will be the new vector?
1.$2\sqrt 2 \widehat j$
2.$2\widehat j$
3.$2\widehat i$
4.$2\sqrt 2 \widehat i$
Answer
561k+ views
Hint: We will first find the angle that $\overrightarrow {OA} $ makes with the $x - $ axis. Then we will rotate $\overrightarrow {OA} $ anticlockwise about the origin and find the new angle. Finally, we will find the $x$ and $y$ components of the new vector and represent it in the form of a vector.
Formula used:
If $O$ is the origin and $A$ is any point such that the vector $\overrightarrow {OA} = x\widehat i + y\widehat j$, then $\left| {\overrightarrow {OA} } \right| = \sqrt {{x^2} + {y^2}} $.
If $\theta $ is the angle that $\overrightarrow {OA} $ makes with the $x - $ axis, then $\tan \theta = \dfrac{y}{x}$.
Complete step-by-step answer:
It is given that $\overrightarrow {OA} = 2\widehat i + 2\widehat j$, where $\widehat i{\text{ and }}\widehat j$ are unit vectors along $x{\text{ and }}y$ respectively.
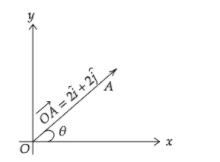
Here, $x - $ component of $\overrightarrow {OA} $ is $2$ and $y - $ component of $\overrightarrow {OA} $ is $2$.
Let $\theta $ be the angle that $\overrightarrow {OA} $ makes with the $x - $ axis. Then,
$ \tan \theta = \dfrac{y}{x} \\
\Rightarrow \tan \theta = \dfrac{2}{2} = 1 \\ $
We know that $\tan 45^\circ = 1$, so substituting this in above equation, we get
$ \Rightarrow \tan \theta = \tan 45^\circ $
$ \Rightarrow \theta = 45^\circ $
Now, let us rotate $\overrightarrow {OA} $ anticlockwise about the origin by $45^\circ $. Let $\alpha $ be the angle that the new vector makes with the $x - $axis.
We observe that
$\alpha = \theta + 45^\circ $
Substituting $\theta = 45^\circ $ in the above equation, we get
$ \Rightarrow \alpha = 45^\circ + 45^\circ \\
\Rightarrow \alpha = 90^\circ \\ $
Let us now find the components of the new vector.
Substituting $x = y = 2$ in the formula $\left| {\overrightarrow {OA} } \right| = \sqrt {{x^2} + {y^2}} $, we get
$\left| {\overrightarrow {OA} } \right| = \sqrt {{2^2} + {2^2}} $
Applying the exponent on the terms, we get
$ \Rightarrow \left| {\overrightarrow {OA} } \right| = \sqrt 8 = 2\sqrt 2 $
The $x - $component of \[\overrightarrow {OA} = \left| {\overrightarrow {OA} } \right|\cos \alpha \widehat i\]
Substituting $\left| {\overrightarrow {OA} } \right| = 2\sqrt 2 $ in the above equation, we get
$\overrightarrow {OA} = 2\sqrt 2 \cos 90^\circ \widehat i$
Now substituting $\cos 90^\circ = 0$ in the above equation, we get
$ \Rightarrow \overrightarrow {OA} = 0\widehat i$
The $y - $component of $\overrightarrow {OA} $ \[ = \left| {\overrightarrow {OA} } \right|\sin \alpha {\text{ }}\widehat j\]
Substituting $\left| {\overrightarrow {OA} } \right| = 2\sqrt 2 $ in the above equation, we get
\[\overrightarrow {OA} = 2\sqrt 2 \sin 90^\circ \widehat j\]
Now substituting $\sin 90^\circ = 1$ in the above equation, we get
\[ \Rightarrow \overrightarrow {OA} = 2\sqrt 2 \widehat j\]
Hence, the new vector $\overrightarrow {OA} = 0\widehat i + 2\sqrt 2 \widehat j = 2\sqrt 2 \widehat j$.
Thus, option (1) is the correct option .
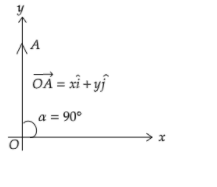
Note: If a vector $\overrightarrow {OA} $ makes an angle $\theta $ with the $x - $axis, then the $x{\text{ and }}y$ components of $\overrightarrow {OA} $ are given as $\left| {\overrightarrow {OA} } \right|\cos \theta $ and $\left| {\overrightarrow {OA} } \right|\sin \theta $ with unit vectors $\widehat i{\text{ and }}\widehat j$ respectively. We have selected the position of $\overrightarrow {OA} $ in the first quadrant since both $x{\text{ and }}y$ components are positive. We can also approach the above problem as follows: After rotating the vector by $45^\circ $, the new vector lies on the $y - $axis. In this case, the $x - $component of the new vector will be zero, which is what we obtained.
Formula used:
If $O$ is the origin and $A$ is any point such that the vector $\overrightarrow {OA} = x\widehat i + y\widehat j$, then $\left| {\overrightarrow {OA} } \right| = \sqrt {{x^2} + {y^2}} $.
If $\theta $ is the angle that $\overrightarrow {OA} $ makes with the $x - $ axis, then $\tan \theta = \dfrac{y}{x}$.
Complete step-by-step answer:
It is given that $\overrightarrow {OA} = 2\widehat i + 2\widehat j$, where $\widehat i{\text{ and }}\widehat j$ are unit vectors along $x{\text{ and }}y$ respectively.

Here, $x - $ component of $\overrightarrow {OA} $ is $2$ and $y - $ component of $\overrightarrow {OA} $ is $2$.
Let $\theta $ be the angle that $\overrightarrow {OA} $ makes with the $x - $ axis. Then,
$ \tan \theta = \dfrac{y}{x} \\
\Rightarrow \tan \theta = \dfrac{2}{2} = 1 \\ $
We know that $\tan 45^\circ = 1$, so substituting this in above equation, we get
$ \Rightarrow \tan \theta = \tan 45^\circ $
$ \Rightarrow \theta = 45^\circ $
Now, let us rotate $\overrightarrow {OA} $ anticlockwise about the origin by $45^\circ $. Let $\alpha $ be the angle that the new vector makes with the $x - $axis.
We observe that
$\alpha = \theta + 45^\circ $
Substituting $\theta = 45^\circ $ in the above equation, we get
$ \Rightarrow \alpha = 45^\circ + 45^\circ \\
\Rightarrow \alpha = 90^\circ \\ $
Let us now find the components of the new vector.
Substituting $x = y = 2$ in the formula $\left| {\overrightarrow {OA} } \right| = \sqrt {{x^2} + {y^2}} $, we get
$\left| {\overrightarrow {OA} } \right| = \sqrt {{2^2} + {2^2}} $
Applying the exponent on the terms, we get
$ \Rightarrow \left| {\overrightarrow {OA} } \right| = \sqrt 8 = 2\sqrt 2 $
The $x - $component of \[\overrightarrow {OA} = \left| {\overrightarrow {OA} } \right|\cos \alpha \widehat i\]
Substituting $\left| {\overrightarrow {OA} } \right| = 2\sqrt 2 $ in the above equation, we get
$\overrightarrow {OA} = 2\sqrt 2 \cos 90^\circ \widehat i$
Now substituting $\cos 90^\circ = 0$ in the above equation, we get
$ \Rightarrow \overrightarrow {OA} = 0\widehat i$
The $y - $component of $\overrightarrow {OA} $ \[ = \left| {\overrightarrow {OA} } \right|\sin \alpha {\text{ }}\widehat j\]
Substituting $\left| {\overrightarrow {OA} } \right| = 2\sqrt 2 $ in the above equation, we get
\[\overrightarrow {OA} = 2\sqrt 2 \sin 90^\circ \widehat j\]
Now substituting $\sin 90^\circ = 1$ in the above equation, we get
\[ \Rightarrow \overrightarrow {OA} = 2\sqrt 2 \widehat j\]
Hence, the new vector $\overrightarrow {OA} = 0\widehat i + 2\sqrt 2 \widehat j = 2\sqrt 2 \widehat j$.
Thus, option (1) is the correct option .
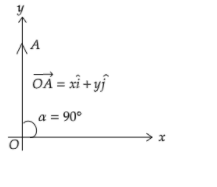
Note: If a vector $\overrightarrow {OA} $ makes an angle $\theta $ with the $x - $axis, then the $x{\text{ and }}y$ components of $\overrightarrow {OA} $ are given as $\left| {\overrightarrow {OA} } \right|\cos \theta $ and $\left| {\overrightarrow {OA} } \right|\sin \theta $ with unit vectors $\widehat i{\text{ and }}\widehat j$ respectively. We have selected the position of $\overrightarrow {OA} $ in the first quadrant since both $x{\text{ and }}y$ components are positive. We can also approach the above problem as follows: After rotating the vector by $45^\circ $, the new vector lies on the $y - $axis. In this case, the $x - $component of the new vector will be zero, which is what we obtained.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




