
The variation of potential energy U of a system is shown in figure. The force acting on the system is best represented by –
A.
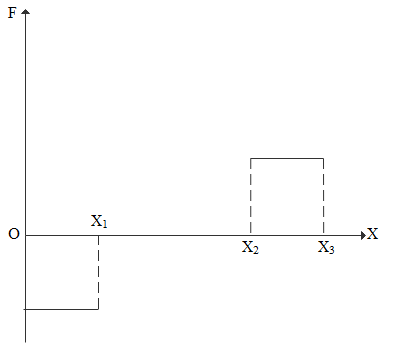
B.
C.
D.

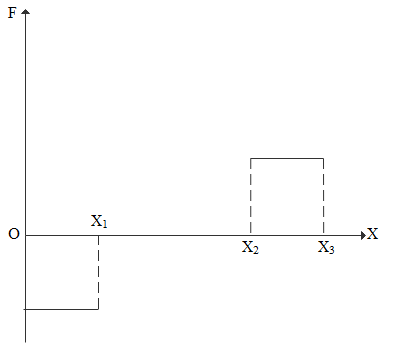



Answer
584.7k+ views
Hint: When we do any work against the conservative force then the work done by us will be stored in the form of potential energy in the system and potential energy increases. Along the direction of conservative force then potential energy of the system decreases.
Formula used:
${F_c} = - \dfrac{{dU}}{{dx}}$
Complete step-by-step answer:
Let us assume there is an object. We are displacing that object up very slowly which means at every instant we can assume its velocity will be zero. When we are moving an object upwards which means that we are displacing the object against the gravitational force. That literally means we are doing some work and according to conservation of energy that work will not go in vain. It will get converted in some form and that is nothing but in the form of potential energy.
If we clearly observe the above case, as the object is moving against gravity i.e as the work done by gravity is negative, the potential energy of the system is increasing.
Hence from the above relation we have the formula ${F_c} = - \dfrac{{dU}}{{dx}}$
${F_c}$ is conservative force and ‘U’ is the potential energy and negative sign indicates that along the direction of conservative force, potential energy of the system decreases.
If we have a plot which is drawn between potential energy(U) and displacement(x) then $\dfrac{{dU}}{{dx}}$ gives us the slope of the graph.
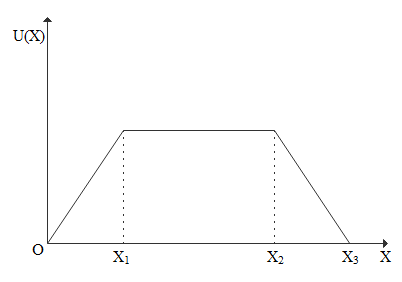
Potential energy and displacement graph is given below.
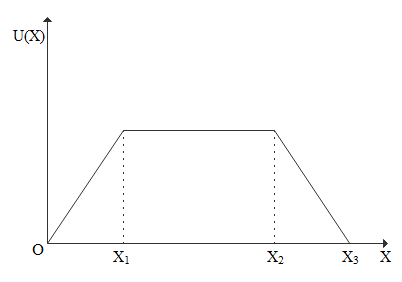
From origin(O) to ${X_1}$ the plot is a straight line with constant positive slope. So in ${F_c} = - \dfrac{{dU}}{{dx}}$ since $\dfrac{{dU}}{{dx}}$ is positive constant $ - \dfrac{{dU}}{{dx}}$ is negative constant so from O to ${X_1}$ force must be constant negative value.
From ${X_1}$ to ${X_2}$ the plot is a straight line with zero slope. So in ${F_c} = - \dfrac{{dU}}{{dx}}$ since $\dfrac{{dU}}{{dx}}$ is zero $ - \dfrac{{dU}}{{dx}}$ will be zero so from ${X_1}$ to ${X_2}$ force must be zero.
From ${X_2}$ to ${X_3}$ the plot is a straight line with constant negative slope. So in ${F_c} = - \dfrac{{dU}}{{dx}}$ since $\dfrac{{dU}}{{dx}}$ is negative constant $ - \dfrac{{dU}}{{dx}}$ is positive constant so from ${X_2}$ to ${X_3}$ force must be constant positive value.
All the characteristics is satisfied by plot A
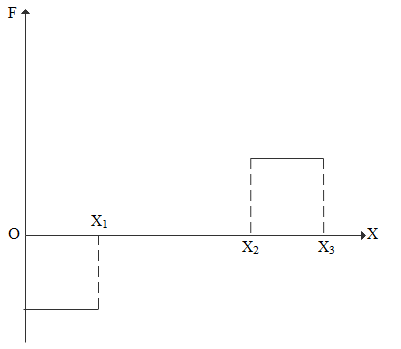
So, the correct answer is “Option A”.
Note: For a straight line slope will be always constant whereas for parabola the slope will be varied from point to point. Slope is nothing but the rate of change of y component with respect to the x component. Potential energy is valid only if conservative forces are present. Gravity, spring force are the examples for conservative forces.
Formula used:
${F_c} = - \dfrac{{dU}}{{dx}}$
Complete step-by-step answer:
Let us assume there is an object. We are displacing that object up very slowly which means at every instant we can assume its velocity will be zero. When we are moving an object upwards which means that we are displacing the object against the gravitational force. That literally means we are doing some work and according to conservation of energy that work will not go in vain. It will get converted in some form and that is nothing but in the form of potential energy.
If we clearly observe the above case, as the object is moving against gravity i.e as the work done by gravity is negative, the potential energy of the system is increasing.
Hence from the above relation we have the formula ${F_c} = - \dfrac{{dU}}{{dx}}$
${F_c}$ is conservative force and ‘U’ is the potential energy and negative sign indicates that along the direction of conservative force, potential energy of the system decreases.
If we have a plot which is drawn between potential energy(U) and displacement(x) then $\dfrac{{dU}}{{dx}}$ gives us the slope of the graph.
Potential energy and displacement graph is given below.

From origin(O) to ${X_1}$ the plot is a straight line with constant positive slope. So in ${F_c} = - \dfrac{{dU}}{{dx}}$ since $\dfrac{{dU}}{{dx}}$ is positive constant $ - \dfrac{{dU}}{{dx}}$ is negative constant so from O to ${X_1}$ force must be constant negative value.
From ${X_1}$ to ${X_2}$ the plot is a straight line with zero slope. So in ${F_c} = - \dfrac{{dU}}{{dx}}$ since $\dfrac{{dU}}{{dx}}$ is zero $ - \dfrac{{dU}}{{dx}}$ will be zero so from ${X_1}$ to ${X_2}$ force must be zero.
From ${X_2}$ to ${X_3}$ the plot is a straight line with constant negative slope. So in ${F_c} = - \dfrac{{dU}}{{dx}}$ since $\dfrac{{dU}}{{dx}}$ is negative constant $ - \dfrac{{dU}}{{dx}}$ is positive constant so from ${X_2}$ to ${X_3}$ force must be constant positive value.
All the characteristics is satisfied by plot A
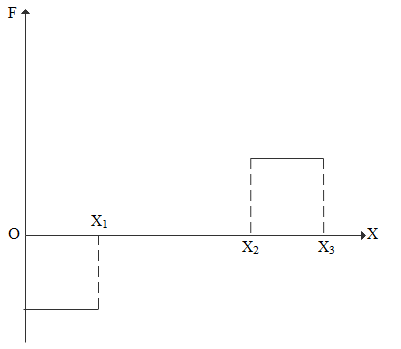
So, the correct answer is “Option A”.
Note: For a straight line slope will be always constant whereas for parabola the slope will be varied from point to point. Slope is nothing but the rate of change of y component with respect to the x component. Potential energy is valid only if conservative forces are present. Gravity, spring force are the examples for conservative forces.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




