Question

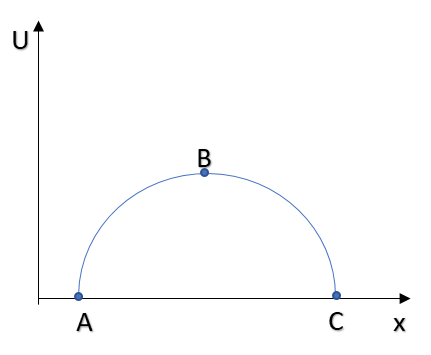
The variation of potential energy U of a body moving along x-axis varies with its position (x) as shown in figure. The body is in equilibrium state at:
A. A
B. B
C. C
D. Both A and C.

Answer 1

Hint: In a conservative field, negative of potential energy is defined as the net force on the particle i.e.$F = -\dfrac{dU}{dx}$, where x is the direction in which particle is moving. Further analyzing the equation, we’ll find that the slope of potential energy and distance will give the measure of slope along with negative sign.

Formula used:
$F = -\dfrac{dU}{dx}$.

Complete answer:
Concept used: A body is said to be in equilibrium if net force on the body is zero. The relation between potential energy and force in a conservative field is given by $F = -\dfrac{dU}{dx}$.
Thus, for the force to be zero, there are three cases:
A. If the potential energy is maximum – This is the condition for unstable equilibrium. In this case, if the body is slightly displaced from its position, it never gets to its original state.
B. If the potential energy is minimum – This is the condition for stable equilibrium. In this case, if the body is slightly displaced from its position, it gets to its original state.
C. If the potential energy is constant – This is the condition for neutral equilibrium. In this case, if the body is slightly displaced from its position, it keeps on moving towards the direction of equilibrium.
Now, seeing the figure, we can say that at B, potential energy is maximum (unstable equilibrium) and force is zero (equilibrium).

So, the correct answer is “Option B”.

Note:
A conservative force is that force in which the work done by the force does not depend upon the path taken i.e. independent of path, called state function. In such types of questions, we are supposed to analyze the slope of the graph, which is the necessary condition for the body to be in equilibrium.