Question

The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below:

I (amperes)	$0.5$	$1$	$2$	$3$	$4$
V(Volts)	$1.6$	$3.4$	$6.7$	$10.2$	$13.2$

Plot a graph between V and I and calculate the resistance of that resistor.

Answer 1

Hint
According to Ohm’s law, a current(I) that flows in a conductor is always proportional to the voltage applied across it (V) and the ratio $\dfrac{V}{I} = R$where R is the constant called Resistance. If the voltage is increased, the current increases, yet Resistance is constant. Thus, the graph plotted will have a constant slope, and the $\tan \theta $will give the value of Resistance.
$\Rightarrow R = \dfrac{V}{I}$Where R is the resistance in conductor, V is the Voltage applied and I is the flowing current.
$\Rightarrow {R_{mean}} = \dfrac{{{R_1} + {R_2} + {R_3} + {R_4} + {R_5}}}{5}$
Equation of a line: $y = mx + c$

Complete step by step answer
We plot the graph between V and I manually which means that a point is marked in the graph wherever the corresponding values of V and I match, there will be a total of 5 points.

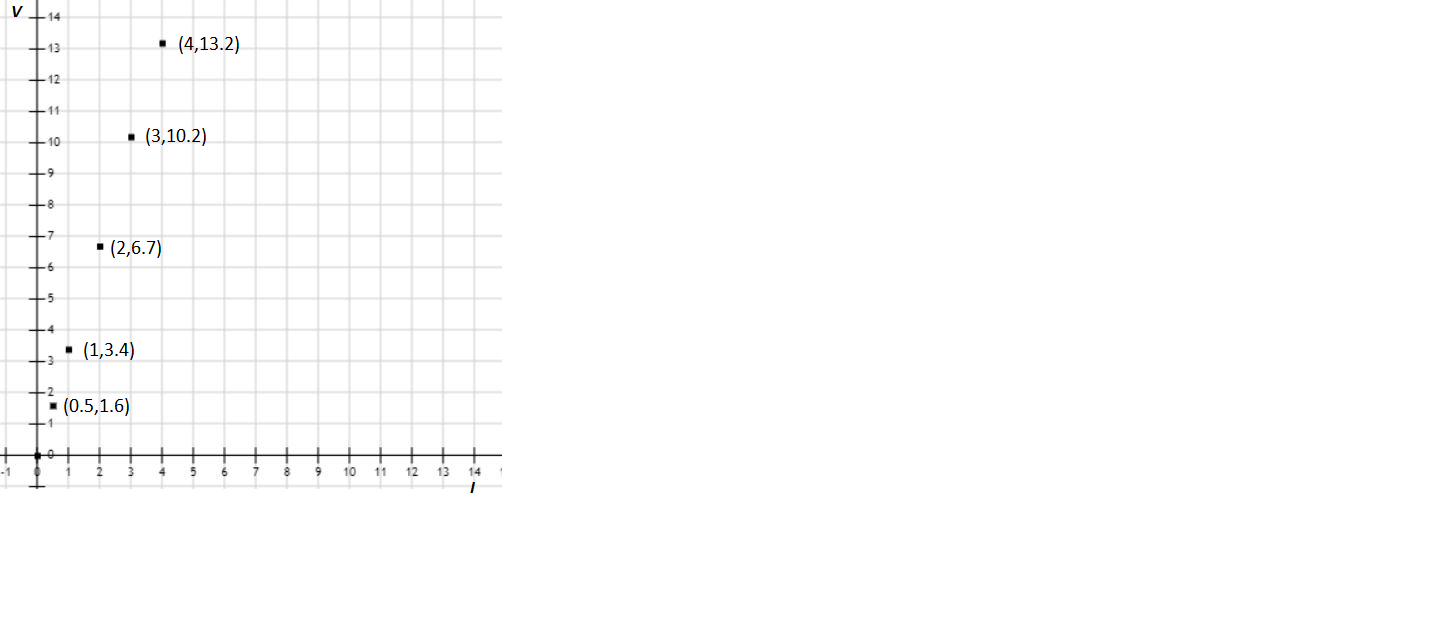
-After this we join all the points, resulting in creation of the graph.

There are 2 methods to solve the resistance, let us see them one by one.
Method 1: We take all 5 values of I and V and calculate 5 values of R
$\Rightarrow {R_1} = \dfrac{V}{I} = \dfrac{{1.6}}{{0.5}} = 3.2\Omega $
$\Rightarrow {R_2} = \dfrac{V}{I} = \dfrac{{3.4}}{1} = 3.2\Omega $
$\Rightarrow {R_3} = \dfrac{V}{I} = \dfrac{{6.7}}{2} = 3.35\Omega $
$\Rightarrow {R_4} = \dfrac{V}{I} = \dfrac{{10.2}}{3} = 3.4\Omega $
$\Rightarrow {R_5} = \dfrac{V}{I} = \dfrac{{13.2}}{4} = 3.3\Omega $
-Now we take the mean of all values of R
$\Rightarrow {R_{mean}} = \dfrac{{3.2 + 3.4 + 3.35 + 3.4 + 3.3}}{5} = \dfrac{{16.85}}{5} = 3.37\Omega $
Thus the Resistance in the conductor is equal to $3.37\Omega $
Method 2: This is a short cut method, it uses the fact that the relation between V and I is linear, which means when plotted, the graph must form a straight line.
Here, you may take any value of I and the corresponding value of V and divide them, but for better accuracy, here we are taking the average values of V and I,
$\Rightarrow {V_{avg}} = \dfrac{{{V_1} + {V_2} + {V_3} + {V_4} + {V_5}}}{5}$
$\Rightarrow {V_{avg}} = \dfrac{{1.6 + 3.4 + 6.7 + 10.2 + 13.2}}{5} = 7.02{\text{V}}$
$\Rightarrow {I_{avg}} = \dfrac{{{I_1} + {I_2} + {I_3} + {I_4} + {I_5}}}{5}$
$\Rightarrow {I_{avg}} = \dfrac{{0.5 + 1 + 2 + 3 + 4}}{5} = 2.1{\text{A}}$
Equation of the line in V-I graph may be compared to,
$\Rightarrow y = mx + c$
$\Rightarrow V = IR + c$
We know that, for V=0, I=0 (When no voltage is applied, no current flows through the conductor)
So,$c = 0$
The equation of line now becomes
$\Rightarrow V = IR$
By putting the values of ${V_{avg}}{\text{ and }}{I_{avg}}$,
$\Rightarrow 7.02 = 2.1 \times R$
$\Rightarrow R = \dfrac{{7.02}}{{2.1}} = 3.34\Omega $.

Note
The accuracy of method 2 may vary according to the accuracy of observation. If the values given in the question are errorless, the answer delivered by method 2 would be the same as in method 1. But in practical, observation has errors (like in this question), therefore the graph will not be a straight line, but will be in the form of zig-zag at a very small scale. So it is better to use Method 1 for the greatest accuracy.