Question

The value of x in the following figure is:

\[
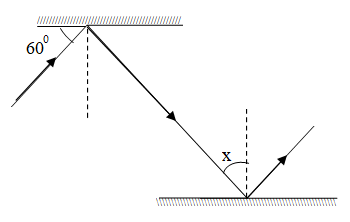
  A.{\text{ }}{30^0} \\
  B.{\text{ }}{45^0} \\
  C.{\text{ 6}}{0^0} \\
  D.{\text{ None of these}} \\
 \]

Answer 1

Hint- In order to solve these questions we will use law or reflection and alternative interior angle property. First use the laws of reflection to find the angles in the upper portion of the figure and then with the help of above angle and alternate interior property move to below part.

Complete step-by-step solution -
Let us use the given figure to solve the problem.

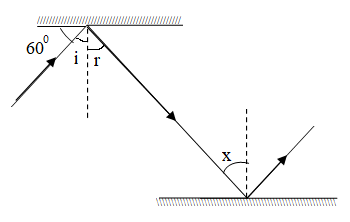
Let us draw an interior angle as “I” and reflection angle as “r”.
According to the law of reflection which states that when a ray of light reflects off a surface, the angle of incidence is equal to the angle of reflection
$ \Rightarrow \angle i = \angle r$
And from the figure
$\angle i = {90^0} - {60^0} = {30^0}$
Therefore, $\angle r = {30^0}$
From the upper and the lower part of the figure we have a pair of parallel mirrors.
As we know that alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. And the alternate interior angles are equal.
So for the given figure.
$ \Rightarrow \angle r = \angle x$
Substitute the value of “r”, as we have found before
$ \Rightarrow \angle x = \angle r = {30^0}$
Hence, the value of x is ${30^0}$
So, option A is the correct option.

Note- The law of reflection states that when a ray of light reflects off a surface, the angle of incidence is equal to the angle of reflection and Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. For solving such practical problems visualize it in terms of some mathematical problem.