Question

The value of the trigonometric expression $\cos {{52}^{\circ }}+\cos {{68}^{\circ }}+\cos {{172}^{\circ }}$ is
A. 0
B. 1
C. 2
D. $\dfrac{3}{2}$

Answer 1

Hint: We first try to break the summation into two parts. We find the sum of $\cos {{68}^{\circ }}+\cos {{172}^{\circ }}$ with the help of $\cos A+\cos B=2\cos \dfrac{A+B}{2}\cos \dfrac{A-B}{2}$. Then we complete the other summation part to get to the solution.

Complete step-by-step solution:
We have addition of three trigonometric ratios. We add them separately.
We have the identity theorem where $\cos A+\cos B=2\cos \dfrac{A+B}{2}\cos \dfrac{A-B}{2}$.
For our given addition of $\cos {{52}^{\circ }}+\cos {{68}^{\circ }}+\cos {{172}^{\circ }}$, we first solve $\cos {{68}^{\circ }}+\cos {{172}^{\circ }}$.
We take $A={{68}^{\circ }},B={{172}^{\circ }}$.
Therefore, $\cos {{68}^{\circ }}+\cos {{172}^{\circ }}=2\cos \dfrac{{{68}^{\circ }}+{{172}^{\circ }}}{2}\cos \dfrac{{{172}^{\circ }}-{{68}^{\circ }}}{2}=2\cos {{120}^{\circ }}\cos {{52}^{\circ }}$.
Now we have to find the value of $\cos {{120}^{\circ }}$.
For general form of $\cos \left( x \right)$, we need to convert the value of x into the closest multiple of $\dfrac{\pi }{2}$ and add or subtract a certain value $\alpha $ from that multiple of $\dfrac{\pi }{2}$ to make it equal to x.
Let’s assume $x=k\times \dfrac{\pi }{2}+\alpha $, $k\in \mathbb{Z}$. Here we took addition of $\alpha $. We also need to remember that $\left| \alpha \right|\le \dfrac{\pi }{2}$.
Now we take the value of k. If it’s even then keep the ratio as cos and if it’s odd then the ratio changes to sin ratio from cos.
Then we find the position of the given angle as quadrant value measured in counter clockwise movement from the origin and the positive side of X-axis.
If the angle falls in the first or fourth quadrant then the sign remains positive but if it falls in the second or third quadrant then the sign becomes negative.
The final form becomes $\cos {{120}^{\circ }}=\cos \left( 1\times \dfrac{\pi }{2}+30 \right)=-\sin \left( 30 \right)=-\dfrac{1}{2}$.
We have $\cos {{52}^{\circ }}+\cos {{68}^{\circ }}+\cos {{172}^{\circ }}=\cos {{52}^{\circ }}+2\left( -\dfrac{1}{2} \right)\cos {{52}^{\circ }}=\cos {{52}^{\circ }}-\cos {{52}^{\circ }}=0$.
The correct option is A.

Note: The choosing of terms for the summation can be arbitrary. We can take $\cos {{52}^{\circ }}+\cos {{68}^{\circ }}$ to find the same solution.
Although we found the associative angle for a particular ratio, the sign of the all-possible trigonometric ratio is positive for the excess angle in their respective quadrants according to the below image.

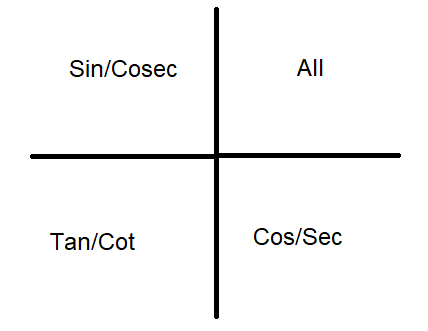
Depending on the sign and ratio change the final angle becomes $\alpha $ from x.