Question

The value of \[\tan {{1}^{\circ }}.\tan {{2}^{\circ }}.\tan {{3}^{\circ }}.\tan {{4}^{\circ }}..........\tan {{89}^{\circ }}\] is:
A. 0
B. 1
C. 2
D. \[\dfrac{1}{2}\]

Answer 1

Hint: First we have to confirm the value of \[\tan \left( {{90}^{\circ }}-\theta \right)=\cot \theta \]. And then use this value on the problem by replacing \[\tan {{87}^{\circ }}.\tan {{88}^{\circ }}.\tan {{89}^{\circ }}\] with \[\tan {{\left( 90-3 \right)}^{\circ }}.\tan {{\left( 90-2 \right)}^{\circ }}.\tan {{\left( 90-1 \right)}^{\circ }}\]. Then we have to use the fundamental multiplication formulae \[\tan \theta .\cot \theta =1\]. And in the middle position there is a \[\tan {{45}^{\circ }}\] hidden. We have to put the value of \[\tan {{45}^{\circ }}=1\] and calculate the rest of the equation accordingly.

Complete step by step solution:
In trigonometric ratios of angles \[\left( {{90}^{\circ }}-\theta \right)\] we can find the relation between all six trigonometric ratios.
Let a rotating line OA rotate about O in the anti-clockwise direction, from initial position to ending position makes an angle \[\angle XOA=\theta \]. Now a point C is taken on OA and drawn CD perpendicular to OX.
Again another rotating line OB rotates about O in the anti-clockwise direction, from initial position to ending position (OX) makes an angle \[\angle XOY={{90}^{\circ }}\]. This rotating line now rotates in the clockwise direction, starting from the position (OY) makes an angle \[\angle YOB=\theta \].
Now, we can observe that \[\angle XOB=\left( 90-\theta \right)\].
Again a point E is taken on OB such that OC = OE and draws EF perpendicular to OX.
Since, \[\angle YOB=\angle XOA\]. Therefore \[\angle OEF=\angle COD\].
Now, from the right-angled \[\vartriangle EOF\] and right-angled \[\vartriangle COD\] we get, \[\angle OEF=\angle COD\] and \[OE=OC\].
Hence \[\vartriangle EOF\cong \vartriangle COD\] (congruent).

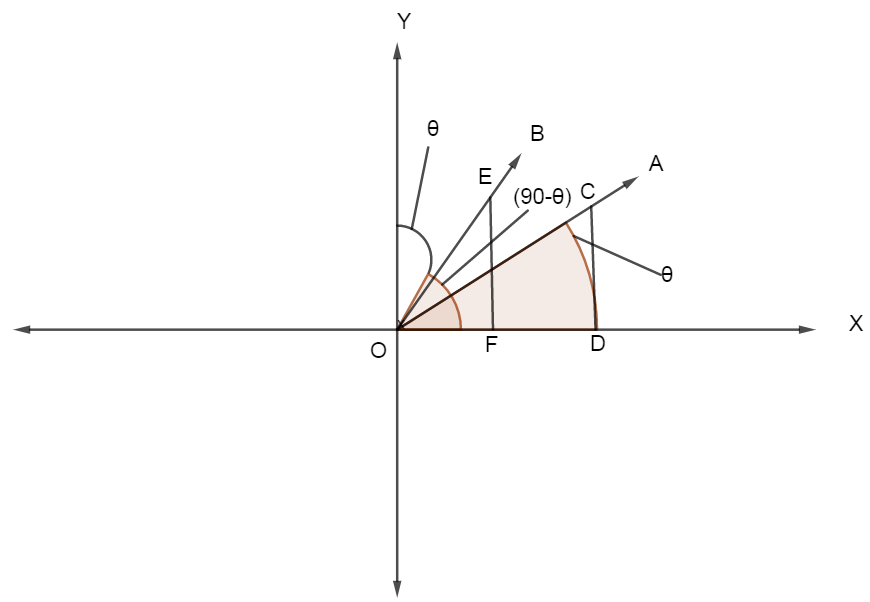
In this diagram FE and OD both are positive. Similarly, OF and DC are both positive.
According to the definition of trigonometric ratio we get,
\[\tan \left( {{90}^{\circ }}-\theta \right)=\cot \theta \]
Now we can write the question as
\[\tan {{1}^{\circ }}.\tan {{2}^{\circ }}.\tan {{3}^{\circ }}......\tan {{87}^{\circ }}.\tan {{88}^{\circ }}.\tan {{89}^{\circ }}\]
In the middle position there is a \[\tan {{45}^{\circ }}\]is hidden,
\[\begin{align}
  & \Rightarrow \tan {{1}^{\circ }}.{{\tan }^{\circ }}\tan {{3}^{\circ }}...\tan {{45}^{\circ }}..\tan {{\left( 90-3 \right)}^{\circ }}.\tan {{\left( 90-2 \right)}^{\circ }}.\tan {{\left( 90-1 \right)}^{\circ }} \\
 & \Rightarrow \tan {{1}^{\circ }}.\tan {{2}^{\circ }}.\tan {{3}^{\circ }}.....\tan {{45}^{\circ }}....\cot {{3}^{\circ }}.\cot {{2}^{\circ }}.\cot {{1}^{\circ }} \\
 & \Rightarrow \tan {{1}^{\circ }}.\cot {{1}^{\circ }}.\tan {{2}^{\circ }}.\cot {{2}^{\circ }}.\tan {{3}^{\circ }}.\cot {{3}^{\circ }}....\tan {{44}^{\circ }}.\cot {{44}^{\circ }}.\tan {{45}^{\circ }} \\
\end{align}\]
We know the value of \[\tan {{45}^{\circ }}=1\] and \[\tan \theta .\cot \theta =1\] we can write
\[\begin{align}
  & \Rightarrow 1\times 1\times 1\times ....\times 1 \\
 & \Rightarrow 1 \\
\end{align}\]
The value of \[\tan {{1}^{\circ }}.\tan {{2}^{\circ }}.\tan {{3}^{\circ }}.\tan {{4}^{\circ }}..........\tan {{89}^{\circ }}\] is 1(option B).

Note: Students have to remember the value of \[\tan {{45}^{\circ }}=1\] and \[\tan \theta .\cot \theta =1\]. Students have to understand how to change \[\tan {{87}^{\circ }}.\tan {{88}^{\circ }}.\tan {{89}^{\circ }}\]into \[\cot {{3}^{\circ }}.\cot {{2}^{\circ }}.\cot {{1}^{\circ }}\]. This step is key to solve this type of question. They have to remember trigonometric ratios of angles \[\left( {{90}^{\circ }}-\theta \right)\] and its relations with trigonometric ratios.