Question

The value of \[\sqrt{0.9}\] is (approx.):
(a) 0.3
(b) 0.6
(c) 0.9
(d) 0.4

Answer 1

Hint: First of all write \[X=\sqrt{0.9}\] as \[X=\sqrt{\dfrac{9}{10}}\] or \[X=\dfrac{\sqrt{9}}{\sqrt{10}}\]. Now further write \[X=\dfrac{3}{\sqrt{10}}\]. Now find the value of \[\sqrt{10}\] by long division method and substitute here to find the value of \[\sqrt{0.9}\].

Complete step-by-step answer:

Here we have to find the approximate value of \[\sqrt{0.9}\]. Let us write the square root of 0.9 as

\[X=\sqrt{0.9}\]

We can write \[0.9=\dfrac{9}{10}\]. So, we get,

\[X=\sqrt{\dfrac{9}{10}}\]

We know that \[\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}\]. So, we get,

\[X=\dfrac{\sqrt{9}}{\sqrt{10}}\]

We know that \[9=3\times 3\]. By substituting the value of 9, we get,

\[X=\dfrac{\sqrt{3\times 3}}{\sqrt{10}}\]

\[X=\dfrac{\sqrt{{{3}^{2}}}}{\sqrt{10}}\]

We know that \[\sqrt{{{a}^{2}}}=a\]. By using this, we get,

\[X=\dfrac{3}{\sqrt{10}}....\left( i \right)\]

Now, to find the value of \[\sqrt{10}\] we will use the long division method. For it, first of all, we will place a bar over the number whose square root is to be found that is 10, starting from unit’s digit in pair of it as

\[\overline{10}.\overline{00}\overline{00}\overline{00}\]

Now, we will take the largest number whose square is less than or equal to 10 as the divisor and that number is 3 as follows:

Now, we will double the value of the divisor and enter it with the blank on the right side as follows

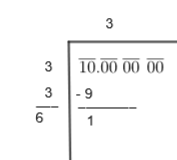
Now, we will take down 2 zeroes and find a number such that (6x)(x) is less than 100 as follows

Now, we will repeat similar steps as follows

So, we have found the approximate value of \[\sqrt{10}\] as 3.162. So, by substituting the value of \[\sqrt{10}\] in equation (i), we get,

\[X=\dfrac{3}{3.162}\]

\[X=0.9487\approx 0.9\]

So, we get the approximate value of \[X=\sqrt{0.9}=0.9\]

Hence, the option (c) is the right answer.


Note: In this question, many students make this mistake of answering 0.3 which is wrong. As \[\sqrt{9}=3\], students assume that \[\sqrt{0.9}\] is also equal to 0.3 but when we multiply 0.3 by 0.3, we get 0.09, not 0.9. So \[\sqrt{0.09}=0.3\] and \[\sqrt{0.9}\ne 0.3\]. So, this must be taken care of.