Question

The value of $\sin \dfrac{\pi }{14}\sin \dfrac{3\pi }{14}\sin \dfrac{5\pi }{14}\sin \dfrac{7\pi }{14}\sin \dfrac{9\pi }{14}\sin \dfrac{11\pi }{14}\sin \dfrac{13\pi }{14}$ is
\[\begin{align}
  & A.\dfrac{1}{16} \\
 & B.\dfrac{1}{64} \\
 & C.\dfrac{1}{128} \\
 & D.\dfrac{1}{32} \\
\end{align}\]

Answer 1

Hint: Here, we apply the concept of trigonometric ratios and identities. Some important trigonometric identities for angles used in this particular question are:
\[\begin{align}
  & \sin \left( \dfrac{\pi }{2}-\theta \right)=\cos \theta \\
 & \sin \left( \dfrac{\pi }{2}+\theta \right)=\cos \theta \\
 & \sin \left( \pi -\theta \right)=\sin \theta \\
 & \sin \left( \pi +\theta \right)=-\sin \theta \\
\end{align}\]
\[\begin{align}
  & \cos \left( \dfrac{\pi }{2}-\theta \right)=\sin \theta \\
 & \cos \left( \dfrac{\pi }{2}+\theta \right)=-\sin \theta \\
 & \cos \left( \pi -\theta \right)=-\cos \theta \\
 & \cos \left( \pi +\theta \right)=-\cos \theta \\
\end{align}\]
Firstly, we will convert the last three terms of the given question according to the first three terms. The middle term becomes 1 $\left( \because \sin \dfrac{7\pi }{14}=\sin \dfrac{\pi }{2}=1 \right)$
Therefore, after combining the all terms and manipulating the values according to above 8 fundamental formulas, we get the constant answer.

Complete step-by-step solution:
Let’s jump to the question, we have:
\[A=\left( \sin \dfrac{\pi }{14}\sin \dfrac{3\pi }{14}\sin \dfrac{5\pi }{14}\sin \dfrac{7\pi }{14}\sin \dfrac{9\pi }{14}\sin \dfrac{11\pi }{14}\sin \dfrac{13\pi }{14} \right)\cdots \cdots \cdots (i)\]
Here, considering the middle term and expressing its value, we have \[\sin \dfrac{7\pi }{14}=\sin \dfrac{\pi }{2}=1\]
Now, let us take the term $\sin \dfrac{9\pi }{14}$ can be written as $\sin \left( \dfrac{14\pi -5\pi }{14} \right)$
\[\begin{align}
  & \therefore \sin \left( \dfrac{14\pi }{14}-\dfrac{5\pi }{14} \right) \\
 & \Rightarrow \sin \left( \pi -\dfrac{5\pi }{14} \right) \\
 & \Rightarrow \sin \left( \dfrac{5\pi }{14} \right)\left( \because \sin \left( \pi -\theta \right)=\sin \theta \right) \\
\end{align}\]
Similarly, for the term $\sin \dfrac{11\pi }{14}$ we can write it as $\sin \left( \dfrac{14\pi -3\pi }{14} \right)$
Now, applying identities and simplifying, we have
\[\begin{align}
  & \therefore \sin \dfrac{11\pi }{14}=\sin \left( \dfrac{14\pi -3\pi }{14} \right) \\
 & \Rightarrow \sin \left( \pi -\dfrac{3\pi }{14} \right) \\
 & \Rightarrow \sin \left( \dfrac{3\pi }{14} \right) \\
\end{align}\]
And now, let us do the same for next term,
\[\begin{align}
  & \sin \dfrac{13\pi }{14}=\sin \left( \dfrac{14\pi -\pi }{14} \right) \\
 & \Rightarrow \sin \left( \pi -\dfrac{\pi }{14} \right) \\
 & \Rightarrow \sin \left( \dfrac{\pi }{14} \right) \\
\end{align}\]
Now, from equation (i) we have,
\[\begin{align}
  & A=\left( \sin \dfrac{\pi }{14}\sin \dfrac{3\pi }{14}\sin \dfrac{5\pi }{14}\times \left( 1 \right)\times \dfrac{5\pi }{14}\sin \dfrac{3\pi }{14}\sin \dfrac{\pi }{14} \right) \\
 & A={{\left( \sin \dfrac{\pi }{14}\cdot \sin \dfrac{3\pi }{14}\cdot \sin \dfrac{5\pi }{14} \right)}^{2}} \\
\end{align}\]
Now, for the next term, we have
\[\begin{align}
  & \sin \dfrac{\pi }{14}=\sin \left( \dfrac{7\pi -6\pi }{14} \right) \\
 & \Rightarrow \sin \left( \dfrac{\pi }{2}-\dfrac{3\pi }{7} \right) \\
 & \Rightarrow \cos \left( \dfrac{3\pi }{7} \right)\left( \because \sin \left( \dfrac{\pi }{2}-\theta \right)=\cos \theta \right) \\
\end{align}\]
Similarly, we can also simplify the below term as
\[\begin{align}
  & \sin \dfrac{3\pi }{14}=\sin \left( \dfrac{7\pi -4\pi }{14} \right) \\
 & \Rightarrow \sin \left( \dfrac{\pi }{2}-\dfrac{2\pi }{7} \right) \\
 & \Rightarrow \cos \left( \dfrac{2\pi }{7} \right) \\
\end{align}\]
And now we have
\[\begin{align}
  & \sin \dfrac{5\pi }{14}=\sin \left( \dfrac{7\pi -2\pi }{14} \right) \\
 & \Rightarrow \sin \left( \dfrac{\pi }{2}-\dfrac{\pi }{7} \right) \\
 & \Rightarrow \cos \left( \dfrac{\pi }{7} \right) \\
\end{align}\]
Hence, combining all the results obtained above, we can write the expression as \[A={{\left( \cos \dfrac{3\pi }{7}\cdot \cos \dfrac{2\pi }{7}\cdot \cos \dfrac{\pi }{7} \right)}^{2}}\]
Now, we will multiply and divide above expression with $\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)$ therefore, we get:
\[\begin{align}
  & A=\dfrac{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \cos \dfrac{3\pi }{7}\cdot \cos \dfrac{2\pi }{7}\cdot \cos \dfrac{\pi }{7} \right)}^{2}} \\
 & A=\dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( 2\sin \dfrac{\pi }{7}\cdot \cos \dfrac{3\pi }{7}\cdot \cos \dfrac{2\pi }{7}\cdot \cos \dfrac{\pi }{7} \right)}^{2}} \\
\end{align}\]
We know, \[\Rightarrow 2\sin \theta \cos \theta =\sin 2\theta \]
Hence, \[2\sin \dfrac{\pi }{7}\cdot \cos \dfrac{\pi }{7}=\left( \sin \dfrac{2\pi }{7} \right)\]
Now, substituting this in the expression, we have
\[\begin{align}
  & A=\dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \sin \dfrac{2\pi }{7}\cdot \cos \dfrac{2\pi }{7}\cdot \cos \dfrac{3\pi }{7} \right)}^{2}} \\
 & A=\dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \dfrac{2}{2}\cdot \sin \dfrac{2\pi }{7}\cdot \cos \dfrac{2\pi }{7}\cdot \cos \dfrac{3\pi }{7} \right)}^{2}} \\
\end{align}\]
Now, multiply and divide by 2 inside the bracket.
\[\begin{align}
  & \therefore 2\sin \dfrac{2\pi }{7}\cdot \cos \dfrac{2\pi }{7}=\sin \dfrac{4\pi }{7} \\
 & \text{And} \\
 & \text{cos}\dfrac{3\pi }{7}=\cos \left( \dfrac{7\pi -4\pi }{7} \right) \\
 & \Rightarrow \cos \left( \pi -\dfrac{4\pi }{7} \right)= - \cos \dfrac{4\pi }{7}\left( \because \cos \left( \pi -\theta \right)=-\cos \theta \right) \\
\end{align}\]
\[\begin{align}
  & \therefore A=\dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \dfrac{1}{2}\times \sin \dfrac{4\pi }{7}\cdot \left( -\cos \dfrac{4\pi }{7} \right) \right)}^{2}} \\
 & \Rightarrow \dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \dfrac{-1}{2\times 2}\times 2\sin \dfrac{4\pi }{7}\cdot \cos \dfrac{4\pi }{7} \right)}^{2}} \\
 & \Rightarrow \dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \dfrac{-1}{4}\times \sin \dfrac{8\pi }{7} \right)}^{2}} \\
 & \Rightarrow \dfrac{1}{\left( 4{{\sin }^{2}}\dfrac{\pi }{7} \right)}{{\left( \dfrac{-1}{4}\times \sin \left( \dfrac{7\pi +\pi }{7} \right) \right)}^{2}} \\
\end{align}\]
We know, \[\sin \left( \pi +\theta \right)=-\sin \theta \]
\[\begin{align}
  & \therefore \sin \left( \dfrac{7\pi +\pi }{7} \right)=\sin \left( \pi +\dfrac{\pi }{7} \right)=-\sin \left( \dfrac{\pi }{7} \right) \\
 & A=\dfrac{1}{4{{\sin }^{2}}\dfrac{\pi }{7}}{{\left( \dfrac{-1}{4}\times \left( -\sin \dfrac{\pi }{7} \right) \right)}^{2}} \\
 & \Rightarrow \dfrac{1}{4{{\sin }^{2}}\dfrac{\pi }{7}}{{\left( \dfrac{1}{4} \right)}^{2}}{{\left( \sin \dfrac{\pi }{7} \right)}^{2}} \\
\end{align}\]
Cancelling ${{\left( \sin \dfrac{\pi }{7} \right)}^{2}}$ we get:
\[\begin{align}
  & \Rightarrow \dfrac{1}{4}\times {{\left( \dfrac{1}{4} \right)}^{2}} \\
 & \Rightarrow \dfrac{1}{64} \\
\end{align}\]
Therefore, B is the correct answer.

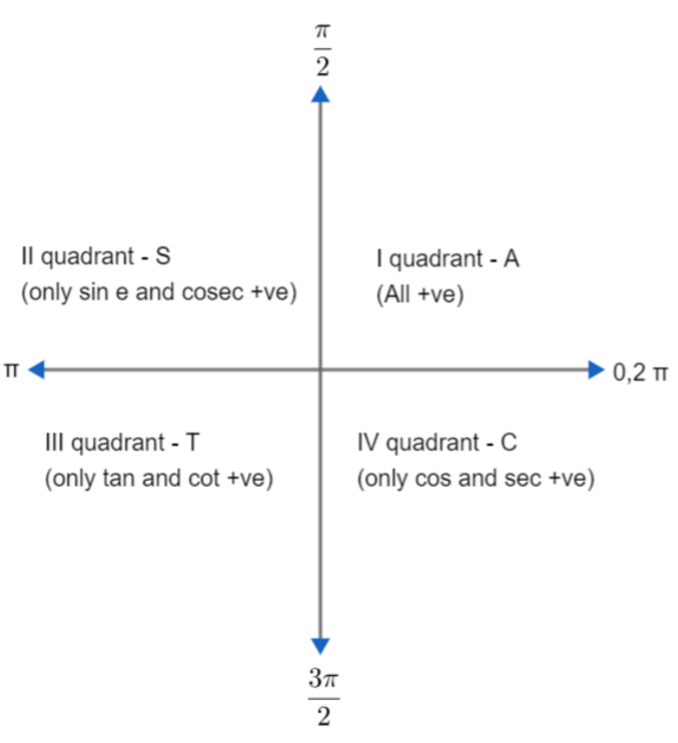
Note: Although the question is solely based on identities and manipulation, if anywhere, we use the wrong positive or negative sign in the identities formula then, we will get the wrong answer. For avoiding such a mistake, we have one table which describes sign representation.