Question

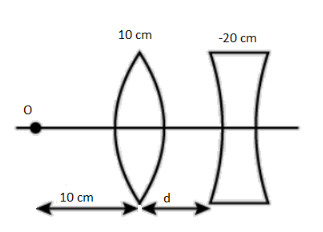
What should be the value of distance \[d\] so that the final image is formed on the object itself. (Focal lengths of the lenses are written on the lenses.)

     

Answer 1

Hint:In this question, we can use the lens formula. In this question, two images are formed. We can calculate the distance of the first image for the convex lens. Then we can calculate the distance of the second image/final image for the concave lens.

Complete step by step solution: -
According to the question, we have two lenses. First one is a convex lens and the second one is a concave lens.

The first image will be formed by the first lens convex lens. Let the image be formed at a distance ${v_1}$ when the object is at point \[O\] at the distance ${u_1} = - 10cm$. We know that the focal length of the convex lens is ${f_1} = 10cm$. So, we can use lens formula for the convex lens which is given as-
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
So, substituting the values for convex lens in the lens formula, we get-
$
  \dfrac{1}{{{v_1}}} - \dfrac{1}{{ - 10}} = \dfrac{1}{{10}} \\
   \Rightarrow \dfrac{1}{{{v_1}}} + \dfrac{1}{{10}} = \dfrac{1}{{10}} \\
   \Rightarrow \dfrac{1}{{{v_1}}} = \dfrac{1}{{10}} - \dfrac{1}{{10}} \\
   \Rightarrow \dfrac{1}{{{v_1}}} = 0 \\
   \Rightarrow {v_1} = \dfrac{1}{0} \\
   \Rightarrow {v_1} = \infty \\
$
Now, the image from the convex lens will become the object for the second lens which is a concave lens.
Now, according to the question, the focal length of the concave lens ${f_2} = - 20cm$ and from the above calculation, we have the distance of object \[{u_2} = {v_1} = \infty \]. Let the distance of the image is ${v_2}$, then using the lens formula, we get-
$
  \dfrac{1}{{{v_2}}} - \dfrac{1}{\infty } = \dfrac{1}{{ - 20}} \\
   \Rightarrow \dfrac{1}{{{v_2}}} - 0 = \dfrac{1}{{ - 20}} \\
   \Rightarrow {v_2} = - 20cm \\
$
So, the final image which is formed by the concave lens is at $ - 20cm$.
Negative sign gives the position of the final image which is formed at the left side of both lenses.
So, the final image is formed at $20cm$.
Now, from the figure, we have-
${v_{_2}} = d + 10cm$
From the above calculations, we have $\left| {{v_2}} \right| = 20cm$. So,
 $
   \Rightarrow 20 = d + 10 \\
   \Rightarrow d = 20 - 10 \\
   \Rightarrow d = 10cm \\
$
Hence, the distance between both the lenses $d = 10cm$.

Note: - In this question, we have to remember that there are two images formed by two lenses. The image from the first lens i.s. convex lens will become the object for the second lens i.e. concave lens.