Question

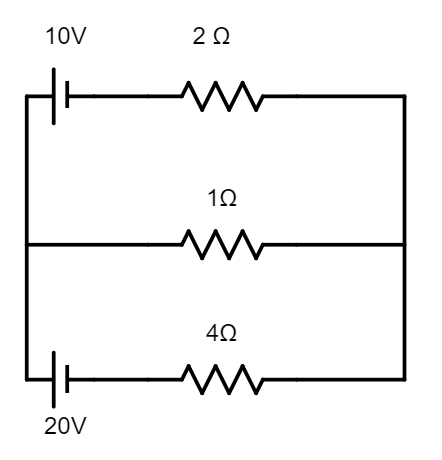
The value of current through $2\Omega $ resistor in the circuit is

A) $10A$
B) $2.1A$
C) $20A$
D) $25A$

Answer 1

Hint: To proceed, we have to apply Kirchhoff’s rules. Kirchhoff’s first rule says that the algebraic sum of the currents meeting at a junction in a closed electric circuit is zero. Kirchhoff’s second rule says that the algebraic sum of change in potential around any closed path of an electric circuit (or closed loop) involving resistors and cells in the loop is zero.

Complete answer:
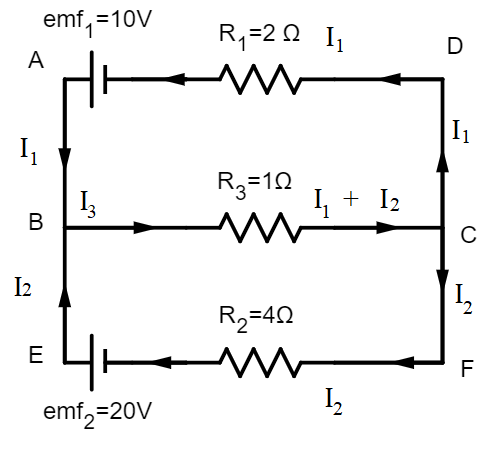
Firstly, let us redraw the circuit by naming the components according to our comfortability.

Let us name the resistors as
${{R}_{_{1}}}=2\Omega $, ${{R}_{2}}=4\Omega $, and ${{R}_{3}}=1\Omega $
Let the currents flowing through resistors ${{R}_{1}},{{R}_{2}},$ and ${{R}_{3}}$ be ${{I}_{1}},{{I}_{2}},$ and ${{I}_{3}}$, respectively.
We are also provided with two electromotive forces. Let us call them $em{{f}_{1}}=10V$ and $em{{f}_{2}}=20V$, respectively.
Kirchhoff’s first rule or current rule (KCL) says that the algebraic sum of the currents meeting at a junction in a closed electric circuit is zero. It says that
$\sum I=0$

Applying this rule in our circuit, we have
${{I}_{3}}={{I}_{1}}+{{I}_{2}}$, at node B as well as node C. Let this be equation 1.
Kirchhoff’s second rule or voltage rule (KVL) says that the algebraic sum of change in potential around any closed path of an electric circuit (or closed loop) involving resistors and cells in the loop is zero. It says that $\sum emf+\sum IR=0$

Applying this rule in closed loop ABCDA, we have
$-em{{f}_{1}}+{{I}_{3}}{{R}_{3}}+{{I}_{1}}{{R}_{1}}=0\Rightarrow -10+({{I}_{1}}+{{I}_{2}})1+{{I}_{1}}(2)=0\Rightarrow ({{I}_{1}}+{{I}_{2}})+2{{I}_{1}}=10\Rightarrow 3{{I}_{1}}+{{I}_{2}}=10$...Let this be equation 2.

Applying the same rule to the loop EBCFE, we have
$-em{{f}_{2}}+{{I}_{3}}{{R}_{3}}+{{I}_{2}}{{R}_{2}}=0\Rightarrow -20+({{I}_{1}}+{{I}_{2}})1+{{I}_{2}}(4)=0\Rightarrow ({{I}_{1}}+{{I}_{2}})+4{{I}_{2}}=20\Rightarrow {{I}_{1}}+5{{I}_{2}}=20$.....Let this be equation 3.

Solving equation 2 and equation 3, we have
${{I}_{2}}=\dfrac{25}{7}A$ and ${{I}_{1}}=\dfrac{15}{7}=2.1A$
Therefore, the current flowing through the resistor,${{R}_{1}}=2\Omega $ is given by ${{I}_{1}}=2.1A$.

So, the correct answer is “Option B”.

Note:
Kirchhoff’s rules follow sign convention. To make it easy, in KCL, the current flowing towards a node is taken as positive and the current flowing away from the node is taken as negative. In KVL, while traversing a loop, if a negative pole of the cell is encountered first, then its emf is negative, otherwise positive.