Question

The value of \[\cos {{90}^{\circ }}\] is ……………….
A) 1
B) 0
C) \[\sqrt{3}\]
D) \[\dfrac{1}{\sqrt{3}}\]

Answer 1

HINT: First of all, we will form a right angled triangle as follows-

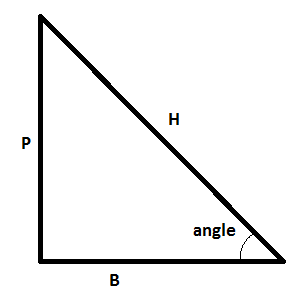
Now, as we know that the value of cos function is as follows
\[\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}\]
In this question, we will try to increase the angle to make it \[{{90}^{\circ }}\] and then we will try to use this formula to get the value of \[\cos \theta \] .

Complete step-by-step answer:
Now, in this question, we have to find the value of \[\cos \theta \] .
Now, as mentioned in the hint, we will increase the angle such that it tends to \[{{90}^{\circ }}\] . we can see that when we will increase the angle to make it to \[{{90}^{\circ }}\] , we can see that on using the formula for getting the value of \[\cos \theta \] becomes \[\cos {{90}^{\circ }}\] and we can write as follows
\[\cos {{90}^{\circ }}=\dfrac{\text{Base}\to 0}{\text{Hypotenuse}}=0\]
(This is because the value of perpendicular becomes \[\infty \])
Hence, the value of \[\cos {{90}^{\circ }}\] comes out to be 0.

NOTE:- Another method of solving this question is that
We know that for \[\sin ({{90}^{\circ }}-x)=\cos x\] . So, we can find the value of \[\cos {{90}^{\circ }}\] as follows
 \[\begin{align}
  & \Rightarrow \cos x=\sin ({{90}^{\circ }}-x) \\
 & \Rightarrow \cos {{90}^{\circ }}=\sin ({{90}^{\circ }}-{{90}^{\circ }}) \\
 & \Rightarrow \cos {{90}^{\circ }}=\sin {{0}^{\circ }} \\
\end{align}\]
Now, if one knows that \[\sin {{0}^{\circ }}=0\], then one can get that the value of \[\cos {{90}^{\circ }}\] is 0.