Question

The value of \[\arg \left( x \right)\] when $x < 0$ is:
A.0
B.$\dfrac{\pi }{2}$
C.$\pi $
D.None of these

Answer 1

Hint: Represent the given complex number on the plane, where the real part corresponds to the $x$ coordinate and the imaginary part corresponds to the $y$ axis. Take $x < 0$. The argument of the angle is the angle in radians, inclined from real axis $\left( {x - axis} \right)$ in the direction of complex number, when complex number is represented on the complex plane

Complete step-by-step answer:
A complex number is of the form $a + ib$, where $a$ is the real part and $b$ represents the imaginary part.
In polar form, a complex number is written as $r\left( {\cos \theta + i\sin \theta } \right)$, where $r$is the modulus of the complex number and $\theta $ is the argument of the complex number.
The argument of the angle is the angle in radians, inclined from the real axis $\left( {x - axis} \right)$ in the direction of complex number, when complex number is represented on the complex plane.
In the given complex number, $z = x$, the real part is $x$ and it has no imaginary part.
Represent the given complex number on the plane.

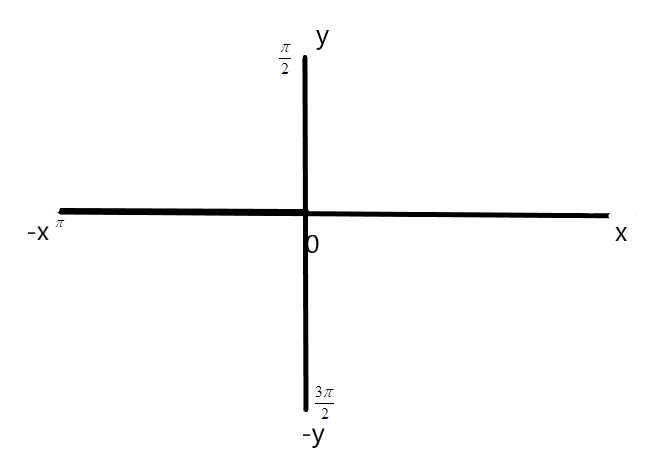
From the figure, the complex number represents the negative $x$ axis.
We have to find the angle inclined from $x - axis$ to the complex number in the direction of the complex number. Since, the value of $x < 0$, we can see from the graph that the value of the argument is $\pi $.
Thus, the value of \[\arg \left( x \right)\] when $x < 0$ is $\pi $.
Hence, option C is correct.


Note: The argument of the complex number is the angle in radians measured from the $x$ axis in an anticlockwise direction. $x$ axis represents the real part and $y$ axis represents the complex part of a complex number.