Question

The upper part of the tree broken over by the wind makes an angle of $ {30^0} $ with the ground, and the distance from the root to the point where the top of the tree meets the ground is 15 meters. The present height of the tree is
A.15 meters
B. $ 10\sqrt 3 $ meters
C.20 meters
D.None of the above

Answer 1

Hint: In this question, we need to evaluate the height of the tree such that the tree has been broken over by the wind which makes an angle of $ {30^0} $ with the ground, and the distance from the root to the point where the top of the tree meets the ground is 15 meters. For this, we will use the trigonometric identities and properties of the triangle to determine the length of the tree.

Complete step-by-step answer:
Let the height of the tree be ‘H’.
According to the data given in the question, the following figure has been made which indicates the mathematical scenario of the situation.

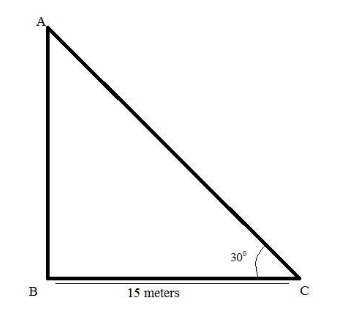
Here, AB is the height of the tree and BC is the distance between the roots of the tree to the point where the top of the tree meets the ground.
Following the tangent of the trigonometric model which is defined as the ratio of the height and the base of the right angle triangle. Mathematically, $ \tan \theta = \dfrac{p}{b} $ where, p is the perpendicular and b is the base of the triangle.
Substituting the known values in the equation $ \tan \theta = \dfrac{p}{b} $ as:
 $
  \tan \theta = \dfrac{p}{b} \\
   \Rightarrow \tan 30 = \dfrac{{AB}}{{BC}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{15}} \\
   \Rightarrow h = \dfrac{{15}}{{\sqrt 3 }} \;
  $
Hence, the height of the tree after it is broken down by the wind is $ \dfrac{{15}}{{\sqrt 3 }} $ meters.
So, the correct answer is “$ \dfrac{{15}}{{\sqrt 3 }} $ meters.”.

Note: It is worth noting down here that the perpendicular and the base of the triangle depends according to the angle we are considering for. The opposite side of the angle in the right angle triangle is always considered to be the perpendicular side while the other one is considered to be as the base.