Question

The upper part of the tree broken over by the wind makes an angle of ${{30}^{\circ }}$ with the ground, and the distance from the root to the point where the top of the tree meets the ground is 15m. The present height of the tree is
(a) $15m$
(b) $10\sqrt{3}m$
(c) $20m$
(d) None of these

Answer 1

Hint: In a right-angled triangle $\Delta ABC$,

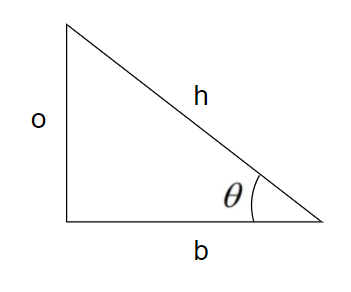
$\sin \theta =\dfrac{opposite}{hypotenuse}=\dfrac{o}{h}$
$\begin{align}
  & \cos \theta =\dfrac{base}{hypotenuse}=\dfrac{b}{h} \\
 & \tan \theta =\dfrac{\sin \theta }{\cos \theta }=\dfrac{o}{b} \\
\end{align}$
Some important trigonometric angles are:
$\begin{align}
  & \sin {{30}^{\circ }}=\dfrac{1}{2} \\
 & \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \\
 & \sin {{45}^{\circ }}=\dfrac{1}{\sqrt{2}} \\
 & \tan {{45}^{\circ }}=1 \\
 & \sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2} \\
 & \tan {{60}^{\circ }}=\sqrt{3} \\
 & \\
\end{align}$

Complete step by step solution:
Here, the question says that the top of the tree broke and fell on the ground making an angle of ${{30}^{\circ }}$ with the ground. Also, the distance of the top of the tree touching the ground to the root of the tree is $15m$. So, the required figure would be
 

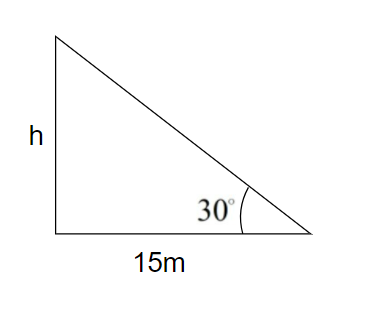
Now, to calculate the present height(h) of the tree, we will use trigonometric ratios and their values at an angle of ${{30}^{\circ }}$.
Considering this figure,
$\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{h}{15} \\
 & \Rightarrow h=15\tan {{30}^{\circ }} \\
\end{align}$
As we know that the value of $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$, we get
$\begin{align}
  & h=15\times \dfrac{1}{\sqrt{3}} \\
 & \Rightarrow h=\dfrac{15}{\sqrt{3}} \\
 & \Rightarrow h=\dfrac{5\times \sqrt{3}\times \sqrt{3}}{\sqrt{3}} \\
 & \therefore h=5\sqrt{3}m \\
 & \\
\end{align}$
So, the correct answer is “Option d”.

Note: In these types of questions, the tricky part is to draw the correct diagram displaying all the values of angles and lengths as mentioned in the question. Always assume that any object standing vertically upright on the ground will always make a right angle with the ground. This allows us to apply the trigonometric ratios applicable on a right-angled triangle. If the diagram drawn is correct and there is no mistake in taking the correct values of trigonometric angles and their corresponding ratios, then you cannot go wrong in obtaining the correct answer.