
The upper part of the tree broken by the wind which makes an angle of \[60^\circ \] with the ground and the distance from the roots to the point where the top of the tree meets the ground is \[20{\text{m}}\]. Find the length of the broken part of the tree.
Answer
583.8k+ views
Hint: Here, we will use the concept of trigonometry by drawing a triangle from the given information. Where a tree is standing from the point which is our perpendicular of the triangle. Also, the base of the triangle will be the distance of that tree on the ground and where the broken part of the tree meets the ground and the Hypotenuse of the triangle will be the broken part of the tree. We will use the formula \[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}\].
Complete step-by-step answer:
Step 1: First of all, we will draw the triangle where \[{\text{A}}\] is a tree which falls from a point \[{\text{B}}\] to the ground with an angle of \[60^\circ \] at the point \[{\text{C}}\] :
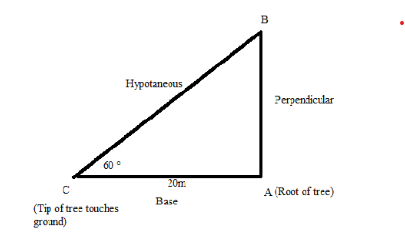
Step 2: We can see from the above diagram that it makes a right-angle triangle where, \[{\text{AB}} = {\text{Perpendicular}}\], \[{\text{AC}} = {\text{Base}} = 20{\text{m}}\] and \[{\text{BC}} = {\text{Hypotenuse}}\].
Step 3: Now by using the formula for \[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}\]:
\[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{AC}}}}{{{\text{BC}}}}{\text{ (}}\because {\text{as given in step 2)}}\]…………….. (1)
The value of the angle \[\angle {\text{ACB = 6}}{{\text{0}}^o}\]also \[{\text{AC}} = 20{\text{m}}\] so, by putting these values in the above expression (1):
\[ \Rightarrow \cos {60^o} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}\]
Step 4: We know that, the value of \[\cos {60^o} = \dfrac{1}{2}\], substituting this value in \[\cos {60^o} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}\] :
\[ \Rightarrow \dfrac{1}{2} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}\]
By taking \[20\]in the LHS side and \[2\]in RHS:
\[ \Rightarrow 20 = 2{\text{AC}}\]
By dividing the LHS side by \[2\]:
\[ \Rightarrow \dfrac{{20}}{2} = {\text{AC}}\]
Thus, solving for \[{\text{AC}}\]:
\[ \Rightarrow {\text{AC}} = 10\]
So, the length of the broken part of the tree is: \[{\text{AC = 10m}}\].
Note: Students should always take the side opposite to the angle as perpendicular and then write the value for corresponding trigonometric functions.
Students should not confuse between sine and cosine value for \[60^\circ \], below are the values for sine, cosine and tan which students should remember:
Complete step-by-step answer:
Step 1: First of all, we will draw the triangle where \[{\text{A}}\] is a tree which falls from a point \[{\text{B}}\] to the ground with an angle of \[60^\circ \] at the point \[{\text{C}}\] :

Step 2: We can see from the above diagram that it makes a right-angle triangle where, \[{\text{AB}} = {\text{Perpendicular}}\], \[{\text{AC}} = {\text{Base}} = 20{\text{m}}\] and \[{\text{BC}} = {\text{Hypotenuse}}\].
Step 3: Now by using the formula for \[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}\]:
\[\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{AC}}}}{{{\text{BC}}}}{\text{ (}}\because {\text{as given in step 2)}}\]…………….. (1)
The value of the angle \[\angle {\text{ACB = 6}}{{\text{0}}^o}\]also \[{\text{AC}} = 20{\text{m}}\] so, by putting these values in the above expression (1):
\[ \Rightarrow \cos {60^o} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}\]
Step 4: We know that, the value of \[\cos {60^o} = \dfrac{1}{2}\], substituting this value in \[\cos {60^o} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}\] :
\[ \Rightarrow \dfrac{1}{2} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}\]
By taking \[20\]in the LHS side and \[2\]in RHS:
\[ \Rightarrow 20 = 2{\text{AC}}\]
By dividing the LHS side by \[2\]:
\[ \Rightarrow \dfrac{{20}}{2} = {\text{AC}}\]
Thus, solving for \[{\text{AC}}\]:
\[ \Rightarrow {\text{AC}} = 10\]
So, the length of the broken part of the tree is: \[{\text{AC = 10m}}\].
Note: Students should always take the side opposite to the angle as perpendicular and then write the value for corresponding trigonometric functions.
Students should not confuse between sine and cosine value for \[60^\circ \], below are the values for sine, cosine and tan which students should remember:
| \[{0^0}\] | \[{30^0}\] | \[{45^0}\] | \[{60^0}\] | \[{90^0}\] | |
| sin | \[0\] | \[\dfrac{1}{2}\] | \[\dfrac{{\sqrt 2 }}{2}\] | \[\dfrac{{\sqrt 3 }}{2}\] | \[1\] |
| cos | \[1\] | \[\dfrac{{\sqrt 3 }}{2}\] | \[\dfrac{{\sqrt 2 }}{2}\] | \[\dfrac{1}{2}\] | \[0\] |
| tan | \[0\] | \[\dfrac{{\sqrt 3 }}{3}\] | \[1\] | \[\sqrt 3 \] | Undefined |
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




