Question

The upper part of a tree had broken by wind, and fell to the ground without being detached. The top of the broken part touches the ground at an angle of ${38^ \circ }30'$ at a point 6 m from the foot of the tree. Calculate:
A) The height at which the tree is broken.
B) The original height of the tree is correct to two decimal places.

Answer 1

Hint: Here in this question we can use trigonometric triangle relations to find out the broken and original height of the tree. Some of the identities are as follows: -

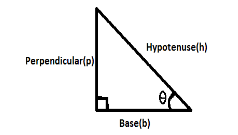
$\sin \theta = \dfrac{p}{h}$
$\tan \theta = \dfrac{p}{b}$
$\cos \theta = \dfrac{b}{h}$

Complete step-by-step answer:
Construction:-With the help of a diagram we will solve this question below is the figure.

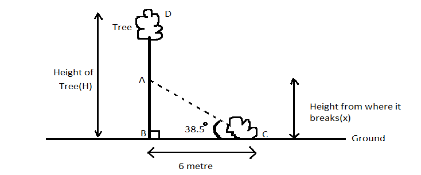
Here H is the original height of the tree before breaking and x is the height after breaking and touching the ground. Tree making an angle with ground is ${38^ \circ }30'$ which can also be read as 38 degree and a half angle so, it can be written as ${38.5^ \circ }$
A) Now we will apply triangle angle property and we will get,
In where $\angle B = {90^ \circ }$ and $BC = 6m$
$ \Rightarrow \tan {38.5^ \circ } = \dfrac{p}{b}$ Where p is perpendicular height and b is base
$ \Rightarrow \tan {38.5^ \circ } = \dfrac{x}{6}$
As we know that $\tan {38.5^ \circ } = 1.03$ so we will put it in the above equation.
$ \Rightarrow 1.03 = \dfrac{x}{6}$
Now we will cross multiply
$ \Rightarrow x = 6.18m$
Therefore height at which tree is broken is 6.18 metres
B) Now if we take where $\angle B = {90^ \circ }$ again and apply Pythagoras theorem in this then we can get the side AC which is the remaining height of the tree we required.
$ \Rightarrow (A{B^2}) + {(BC)^2} = {(AC)^2}$
AB=6.18m, BC=6m and AC we have to find out.
$ \Rightarrow ({6.18^2}) + {(6)^2} = {(AC)^2}$
$ \Rightarrow (38.1924) + (36) = {(AC)^2}$
Now we will open and add the squared terms.
$ \Rightarrow {(AC)^2} = 74.1924$
Now we will do square root of 74.1924
$ \Rightarrow AC = \sqrt {74.1924} = 8.613m$
Therefore the original height of the tree is DA+AB where DA is equal to AC.
$ \Rightarrow DA + AB = 8.613 + 6.18 = 14.793m$.

Note: When you are applying a trigonometric triangle be cautious about base and perpendicular. Base is that side which contains two right angles and one more angle while the perpendicular side consists of only one angle i.e. ninety degrees.