Question

The upper \[{{\dfrac{3}{4}}^{th}}\] portion of a vertical pole subtends an angle \[{{\tan }^{-1}}\dfrac{3}{5}\] at a point in the horizontal plane through its foot and at a distance 40 m from its foot. Given the vertical pole is at height less than 100 m from the ground. Find its height.

Answer 1

Hint: First, we will draw the diagram as per the given data. So, we will get as

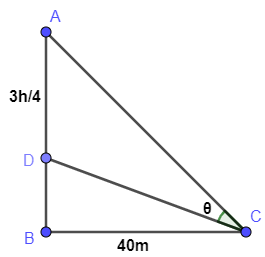
Now, here we will find the height of DB assuming the height of vertical pole to be h. Then, we will use the trigonometric rule i.e. \[\tan \theta =\dfrac{opposite}{adjacent}\] for the triangle \[\Delta ACB\] using the concept \[\angle ACB=\angle ACD+\angle DCB\] . So, we will get the equation as \[\tan \left( \theta +\alpha \right)=\dfrac{AB}{BC}\] . We will solve this using the formula \[\tan \left( \alpha +\beta \right)=\dfrac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }\] and substituting proper values. Thus, on solving we will get the value of height as asked in the question.

Complete step by step answer:
Here, we will first draw the diagram as per the given data in question.

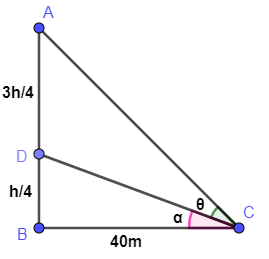
The vertical pole is AB with total height h i.e. \[\dfrac{3h}{4}+\dfrac{h}{4}\] . The angle \[\angle ACD=\theta \] i.e. \[\theta ={{\tan }^{-1}}\dfrac{3}{5}\] is given. The upper portion AD is given as \[\dfrac{3h}{4}\] so, the remaining portion DB will be equal to \[h-\dfrac{3h}{4}=\dfrac{h}{4}\] . We will assume \[\angle DCB=\alpha \] .
Now, we can write \[\theta ={{\tan }^{-1}}\dfrac{3}{5}\] as \[\tan \theta =\dfrac{3}{5}\] . We know that \[\tan \theta =\dfrac{opposite}{adjacent}\] . So, on substituting the value in \[\Delta DCB\] , we get
\[\tan \theta =\dfrac{opposite}{adjacent}\]
\[\tan \alpha =\dfrac{DB}{BC}\]
\[\tan \alpha =\dfrac{h}{4\times 40}=\dfrac{h}{160}\] ………………………………..(1)
Now, in \[\Delta ACB\] we can write \[\angle ACB=\angle ACD+\angle DCB\] . So, we can write \[\tan \left( \theta +\alpha \right)\] using the formula \[\tan \theta =\dfrac{opposite}{adjacent}\] . So, we can write it as
\[\tan \left( \theta +\alpha \right)=\dfrac{AB}{BC}\]
We will use formula of \[\tan \left( \alpha +\beta \right)=\dfrac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }\] . So, using this value we can write it as
\[\dfrac{\tan \theta +\tan \alpha }{1-\tan \theta \tan \alpha }=\dfrac{AB}{BC}\]
Now, we will substitute the values so, we will get as
\[\dfrac{\dfrac{3}{5}+\dfrac{h}{160}}{1-\dfrac{3}{5}\cdot \dfrac{h}{160}}=\dfrac{h}{40}\]
On taking LCM and further simplification, we can get equation as
\[\dfrac{\dfrac{h+96}{160}}{\dfrac{800-3h}{800}}=\dfrac{h}{40}\]
So, we can the denominator term as
\[\dfrac{h+96}{160}\times \dfrac{800}{800-3h}=\dfrac{h}{40}\]
\[\left( h+96 \right)\times \dfrac{5}{800-3h}=\dfrac{h}{40}\]
On further solving, we will get equation as
\[200\left( h+96 \right)=800h-3{{h}^{2}}\]
\[200h+19200=800h-3{{h}^{2}}\]
Taking all the terms on LHS and solving, we will get
\[3{{h}^{2}}-600h+19200=0\]
Now, we will take 3 common from all the terms so, we will get
\[{{h}^{2}}-200h+6400=0\]
Now, we will find the factors of this quadratic equation by splitting the middle term and we will get as
\[{{h}^{2}}-160h-40h+6400=0\]
Taking common terms from the equation. We will get
\[h\left( h-160 \right)-40\left( h-160 \right)=0\]
\[\left( h-40 \right)\left( h-160 \right)=0\]
Thus, we have two values for h i.e. \[h=40,h=160\] .
We are given that the vertical pole is at height less than 100 m from the ground, so height value will be equal to 40 m.
Thus, height is 40 m.

Note: Do not make mistakes in taking the vertical side as pole. Sometimes students draw the diagram as

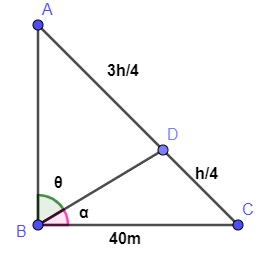
This is the wrong diagram in which hypotenuse is considered as a pole. On solving this there are chances of getting an answer correct but the concept of the question is drawn incorrect. So, the answer will be wrong at last. So, do not make this mistake as the hypotenuse and vertical side is not the same. Secondly, be careful while selecting the value of h because we are getting both the values positive but there is a condition given in question. So, select the answer accordingly.