Question

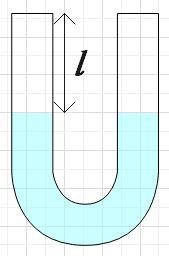
The U tube having identical limbs contains mercury (density ${{\rho }_{m}}$ ) to a level as shown in the figure. If the left limb is filled to the top with water $\left( {{\rho }_{w}} \right)$, then the rise of mercury level in the right limb will be

A. $\dfrac{l}{2{{\rho }_{m}}}$
B. $\dfrac{l{{\rho }_{w}}}{2{{\rho }_{m}}+{{\rho }_{w}}}$
C.$\dfrac{{{\rho }_{m}}l}{{{\rho }_{w}}}$
D.$\dfrac{l{{\rho }_{w}}}{2{{\rho }_{m}}-{{\rho }_{w}}}$

Answer 1

Hint: We know that the rise in mercury in the right limb and the fall in mercury in the left limb due to the filling of water in that limb will be the same. Now you may recall Pascal’s law and thus find that the pressure at the same height is the same. Now keeping that in mind find the expression for gauge pressure for arbitrary points in both limbs and thus find the required rise.
Formula used:
Gauge pressure,
$P-{{P}_{0}}=\rho gh$

Complete step-by-step solution
We are given a U tube that has identical limbs and the U tube has mercury of density ${{\rho }_{m}}$ up to a level. Now we are filling the left limb with water of density ${{\rho }_{w}}$ and we are asked to find the rise in mercury on the right limb.
We know that when we fill water in the left limb up to the brim, there will be a fall in mercury in that limb. Let them fall in mercury in the left limb be given by x, then the rise in mercury in the right limb will be also x as U tube has identical limbs.

Let us consider two points A and B, in the left limb up to the level of point A, water is filled.
We know from Pascal’s law that the pressure at the same height in a liquid is the same. Let the pressure at point A be ${{P}_{A}}$ and that at point B be ${{P}_{B}}$. Now we have the gauge pressure which is given by,
$P-{{P}_{0}}=\rho gh$
Where ‘${{P}_{0}}$’ is the atmospheric pressure.
For point A,
${{P}_{A}}-{{P}_{0}}={{\rho }_{w}}g\left( l+x \right)$ …………………………. (1)
For point B,
${{P}_{B}}-{{P}_{0}}={{\rho }_{m}}g\left( 2x \right)$ …………………………………. (2)
But, ${{P}_{A}}={{P}_{B}}$
Equating RHS of (1) and (2),
${{\rho }_{w}}g\left( l+x \right)={{\rho }_{m}}g\left( 2x \right)$
$\Rightarrow {{\rho }_{w}}l+{{\rho }_{w}}x=2x{{\rho }_{m}}$
$\Rightarrow x\left( 2{{\rho }_{m}}-{{\rho }_{w}} \right)={{\rho }_{w}}l$
$\therefore x=\dfrac{{{\rho }_{w}}l}{2{{\rho }_{m}}-{{\rho }_{w}}}$
Therefore, we find the rise of mercury level in the right limb as,
$x=\dfrac{l{{\rho }_{w}}}{2{{\rho }_{m}}-{{\rho }_{w}}}$
Hence, option D is the correct answer.

Note: The pressure P below the surface of a liquid that is open to the atmosphere is known to be greater than the atmospheric pressure by an amount $\rho gh$. This excess pressure is called gauge pressure. Also, note that the pressure at point A on the interface of water and mercury is due to the water column of height $\left( l+x \right)$ above it and that at the other limb is due to $\left( 2x \right)$ height of mercury above it.