Question

The two opposite vertices of a square are (−1,2) and (3,2). Find the coordinates of the other two vertices.

Answer 1

Hint: In this particular type of question firstly we need to find the value of x using distance formula $\left( {{\text{distance between }}\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right){\text{ = }}\sqrt {{{\left( {{x_1} - {y_1}} \right)}^2} + {{\left( {{x_2} - {y_2}} \right)}^2}} } \right)$ in AB and BC. Then we need to proceed by using Pythagoras theorem in $\vartriangle ABC$ and find the values of y to get the coordinates of opposite vertices of the square.

Complete step-by-step answer:

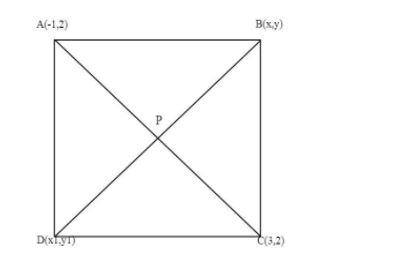
Let ABCD is a square where two opposite vertices are A(−1,2) and C(3,2).
Let B(x,y) and D(${x_1},{y_1}$) be the other two vertices.
In Square ABCD
AB=BC=CD=DA
Hence AB=BC
$\sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 2} \right)}^2}} = \sqrt {{{\left( {3 - x} \right)}^2} + {{\left( {2 - y} \right)}^2}} $ (by distance formula)
Squaring both sides

$
\Rightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {3 - x} \right)^2} + {\left( {2 - y} \right)^2} \\
\Rightarrow {x^2} + 1 + 2x + {y^2} + 4 - 4y = 9 + {x^2} - 6x + 4 + {y^2} - 4y \\
\Rightarrow 2x + 5 = 13 - 6x \\
\Rightarrow 2x + 6x = 13 - 5 \\
\Rightarrow 8x = 8 \\
\Rightarrow x = 1 \\
$

In △ABC, $\angle B = 90^\circ $
(All angles of the square are $90^\circ $)
Then according to the Pythagoras theorem
$

A{B^2} + B{C^2} = A{C^2} \\

\Rightarrow 2A{B^2} = A{C^2}{\text{ }}\left( {{\text{since AB = BC}}} \right) \\

\Rightarrow 2{\left( {\sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 2} \right)}^2}} } \right)^2} =

{\left( {\sqrt {{{\left( {3 - {{\left( { - 1} \right)}^2}} \right)}^2} + {{\left( {2 - 2} \right)}^2}} } \right)^2} \\
\Rightarrow 2\left( {{{\left( {x + 1} \right)}^2} + {{\left( {y - 2} \right)}^2}} \right) = {\left( {3 + 1} \right)^2} + {\left( {2 - 2} \right)^2} \\
\Rightarrow 2\left( {{x^2} + 2x + 1 + {y^2} + 4 - 4y} \right) = {4^2} \\
{\text{put x = 1}} \\
\Rightarrow {\text{2}}\left( {{1^2} + 2 + 1 + {y^2} + 4 - 4y} \right) = 16 \\
\Rightarrow 2\left( {{y^2} - 4y + 8} \right) = 16 \\
\Rightarrow 2{y^2} - 8y + 16 = 16 \\
\Rightarrow 2{y^2} - 8y = 0 \\
\Rightarrow 2y\left( {y - 4} \right) = 0 \\
y = 0,4 \\
$
Therefore the other two vertices of square ABCD are (1,0) and (1,4).

Note: Remember to recall the basic properties of square, Pythagoras theorem and distance formula while solving this type of question. Note that there are two values of y but only one of x, which means the opposite vertices B and D have the same coordinate of x but different coordinates of y. This question could also be solved by using $\vartriangle ACD$ and applying the distance formula and Pythagoras theorem in the same way.