Question

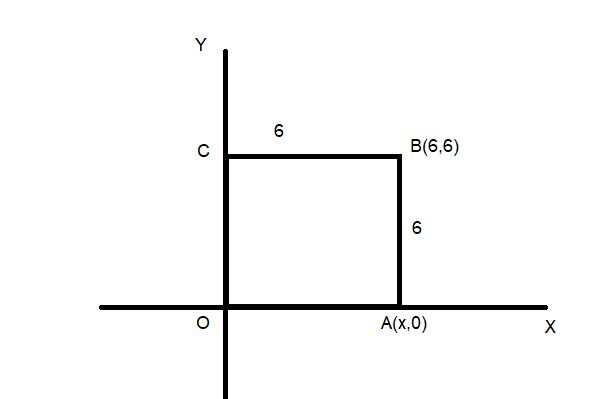
The two diagonally opposite vertices of a square are (6,6) and (0,0). Find the point which lies on X-axis.
$
  {\text{A}}{\text{. }}\left( {6,0} \right) \\
  {\text{B}}{\text{. }}\left( {0,6} \right) \\
  {\text{C}}{\text{. }}\left( {6,6} \right) \\
  {\text{D}}{\text{. None}} \\
$

Answer 1

Hint: To understand this question properly first you have to draw a suitable diagram and apply the property of square that all sides of the square are equal. So using distance formula equate the sides of the square and find the point on the x axis.

Complete Step-by-Step solution:
We have a square OABC and we know all sides of the square are equal.
So OA =AB=BC=OC =sides of square.
Let coordinates of A is (x,0)
From distance formula
 $
  {\text{AB = }}\sqrt {{{\left( {6 - x} \right)}^2} + {{\left( {0 - 6} \right)}^2}} \\
  36 = {\left( {6 - x} \right)^2} + 36 \\
  0 = {\left( {6 - x} \right)^2} \\
  \therefore x = 6 \\
 $
Hence, the point lying on the x axis is A=(6,0)

Note: We have to start from the diagram as told in the hint to start the question. To proceed further and to find the point on the x axis we have to assume a point and use distance formula to get that point. Or we may use the property of angles that all angles are 90 so multiplication of slope of any two continuous sides is -1.