Question

The trunk of a tree is a right circular cylinder 1.5m in radius and 10m high. What is the volume of timber which remains when the trunk is trimmed just enough to reduce it to a rectangular parallelogram on a square base.
A. 45${m^3}$
B. 54${m^3}$
C. 50${m^3}$
D. 48${m^3}$

Answer 1

Hint – In such questions we need to visualize the solid figure and make a rough figure in order to observe the required quantity and way to obtain it as in this question we need to know the basic formulae of volume of solid figures.

Complete step-by-step answer:

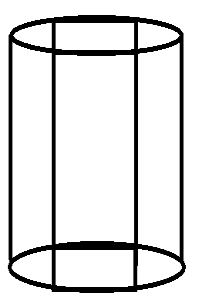
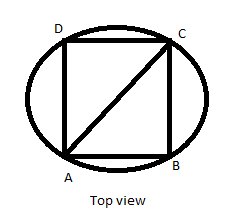
Given,
Radius of cylindrical trunk=1.5m
Height of trunk=10m
In $\Delta ABC$
Radius of trunk=$\sqrt {2{{(side)}^2}} $
$
  A{C^2} = A{B^2} + B{C^2}^{} \\
  {(2R)^2} = 2{(AB)^2} \\
  4{R^2} = 2A{B^2} \\
  4 \times {(1.5)^2} = 2A{B^2} \\
  A{B^2} = 2 \times 2.25 \\
  AB = 2.12m \\
 $
Hence the side of square is 2.12m
Therefore, volume of trimmed trunk=Area of square X height of trunk
Area of square= ${(side)^2}$ =$
  {(2.12)^2} \\
   = 4.49{m^2} \\
$
Volume of trimmed trunk =4.49 X 10
=44.9${m^3}$
$ \cong 45{m^3}$
Hence the answer to this question is $45{m^3}$.

Note – As you could see in the solution that here we needed to find the volume of the remained timber and not the removed timber therefore we have calculated the volume of the rectangular parallelogram on a square base , There are chances that students mind up calculating the the volume or area of the removed timber therefore reading the question properly is must.