Question

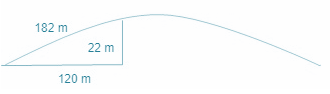
The triangular side walls of a flyover have been used for advertisements. The sides of walls are$122\text{ m, 22m }\!\!\And\!\!\text{ 120m}$ (see figure 12.9). The advertisements yield the earning of Rs 5000 per${{\text{m}}^{2}}$ year. A company hired one of its walls for 3 months. How much rent did it pay?

Answer 1

Hint:
We use Heron's formula for solving the problem. Three sides are given. Also after finding the area cost of advertisement is given we convert the cost for 3 months and multiplied it by area of triangle to get the total rent
Formula used:
Area of triangle$=\sqrt{\text{s}\left( \text{s}-\text{a} \right)\left( \text{s}-\text{b} \right)\left( \text{s}-\text{c} \right)}$
S=Semi perimeter:$\text{s}=\dfrac{\text{a}+\text{b+c}}{2}$

Complete step by step solution:
 The sides of triangle are $122\text{ m, 22m }\!\!\And\!\!\text{ 120m}$
Let a=$122\text{ m}$
b=$120\text{ m}$
c=$22\text{ m}$
 $\begin{align}
  & \text{s}=\dfrac{\text{a}+\text{b+c}}{2} \\
 & =\dfrac{122+120+22}{2} \\
 & =\dfrac{264}{2} \\
 & =132\text{ m} \\
\end{align}$
Area of triangular wall$=\sqrt{\text{s}\left( \text{s}-\text{a} \right)\left( \text{s}-\text{b} \right)\left( \text{s}-\text{c} \right)}$
               $\begin{align}
  & =\sqrt{132\left( 132-122 \right)\left( 132-120 \right)\left( 132-22 \right)} \\
 & =\sqrt{132\times 10\times 12\times 110} \\
 & =\sqrt{11\times 12\times 10\times 12\times 11\times 10} \\
\end{align}$
               $\begin{align}
  & =\sqrt{11\times 12\times 12\times 12\times 10\times 10} \\
 & =\sqrt{{{\left( 11\times 12\times 10 \right)}^{2}}} \\
 & =11\times 12\times 10 \\
 & =1320\text{ m} \\
\end{align}$
Rent of $1\text{ }{{\text{m}}^{2}}$ area$=5000\text{ Rs}$ per year
Rent of $1\text{ }{{\text{m}}^{2}}$ area$=\dfrac{5000}{12}\text{ Rs}$ per month=$\dfrac{1250}{3}\text{ Rs}$per month
For 3 month rent of $1\text{ }{{\text{m}}^{2}}$ area$\dfrac{1250}{3}\text{ }\times \text{3 Rs}$ per quarter=1250
So total rent of $1320\text{ }{{\text{m}}^{2}}$ area for 3 months$=1250\times 320$
$=1650000\text{ Rs}$

So total amount company has to pay as rent$=1650000\text{ Rs}$

Additional information: if the triangle is right angled triangle then we can directly used the formula
Area of triangle$=\dfrac{1}{2}\times \text{base}\times \text{altitude}$

Note:
The knowledge of the basics formula is important for students to solve the question. Also they should know how to convert in per month & in per quarter.